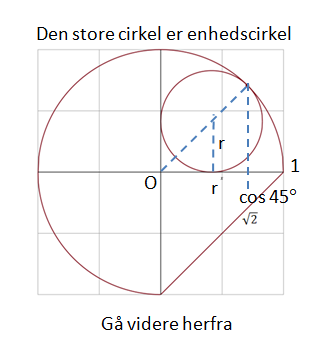
Bestem radius og centrum for den mindste cirkel.

Bestem radius R af den store cirkel med Pythagoras: R² + R² = √2

Bestem den trekant som den lille cirkel er indskrevet i ved at forlænge x- og y- aksen ud til skæringen med tangentet til, hvor de to cirkler tangerer. Den trekant kan deles op i to halve trekanter og igen med pythagoras kan hyptonusens længde L bestemmes med R² + R² = L².

.

(cos 45º , sin 45º) er fælles punkt for de to cirkler.
Centrum for lille cirkel (r , r)
Lille cirkelligning   (r - x)² + (r - y)² = r²
Indsættes heri fællespunktet fås  r =

#2. Den lille retvinklede ligebenede trekant har hypotenusen 1 - r. Pythagoras sætning giver:

(1 - r)² = 2·r² ⇔

1 - 2·r - r² = 0 ⇔

r = 1 ± √2 

Da radius skal være positivt, så er den 1 + √2, og centrum er (1 + √2, 1 + √2)

r skal være mindre end ¹/₂.

#4...rettelse...

(1 - r)² = 2·r² ⇔

- r² - 2·r  + 1 = 0 ⇔

r = -1 ± √2 

Da radius skal være positivt, så er den √2 - 1, og centrum er derfor (√2 - 1, √2 - 1)

Hej, tak for svarene. Jeg har lige et spørgsmål. Hvordan kommer man herfra:

(1 - r)² = 2·r² ⇔

til her:

- r² - 2·r  + 1 = 0 ⇔

også til her:

r = -1 ± √2 

Og er der en matematisk forklaring på hvorfor hypotesnusen for den lille trekant i cirklen er 1-r?

Jeg har fundet ud af hvordan man kommer herfra: (1 - r)² = 2·r² til her r = -1 ± √2. 

Så jeg har kun brug for en matematisk forklaring på hvorfor hypotesnusen for den lille trekant i cirklen er 1-r?

#8. Det skulle fremgå af nedenstående tegning. C er centrum i de indskrevne cirkel. Bemærk at |OB| = 1.