Basis for et vektorrum (i emnet lineære afbildninger).

Enhedsvektor for v er defineret  v/|v|

Rigtig mange tak! Også for det hurtige svar:) 

Når jeg har fundet en enhedsvektor for en af de tre vektorer, der udspænder vektorrummet W, siges den fundne enhedsvektor da at være en basis for vektorrummet? Eller er det forkert forstået?

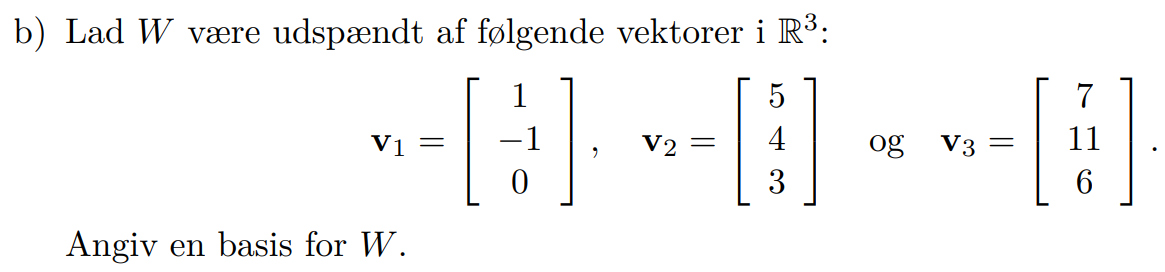
Vi får de tre basisvektorer som enhedsvektorer:
v₁/|v₁| = [1/√(1² + (- 1)² + 0²)]·v₁           og analogt for de to andre.
Alle tre enhedsvektorer udgør basen, en vektor for hver retning i rummet.
Et punkt med stedvektoren OP i rummet kan entydigt bestemmes ved
OP = xv₁/|v₁| + yv₂/|v₂| + zv₃/|v₃|

#3

Mange tak endnu engang. Nu er jeg helt med :)

#3 (rettet version)

I forhold til det, der er tilføjet til #3.

"Alle tre enhedsvektorer udgør basen, en vektor for hver retning i rummet." Skal det forstås på den måde, at basen består af (i dette tilfælde, i R³) består af tre basisvektorer, der hver især er givet ved enhedsvektoren?

Når jeg i opgaven skal angive en basis, skal det vel forstås som en af de tre basisvektorer?

Nej, det skal forstås som alle basisvektorerne. Det er disse basisvektorer som danner hele basen, som er en mængde.

#6

Supergodt, lige at få på plads. Mange tak for svaret:)

Vis, at når
 v₁ , v₂ og v₃ er en basis for W ∧ ∀a ∈ W        ⇔
a kan på en og kun en måde skrives som en linearkombination af v₁ , v₂ og v₃ .