Kemi
Braggs lov - CsCl struktur
Hej
Jeg sidder med en opgave med et stof, som har CsCl-struktur.
Man får oplyst at θ011=16,50 og λ=1,5406 Å
Ud fra dette skal man finde kantlængden.
Jeg har fundet frem til at d=2,714 Å
Håber, at nogen kan hjælpe mig :)
Svar #1
03. august 2014 af bbdk
Har du ikke fået andre oplysninger end det? Hvilket stof og hvad er densiteten f.eks?
Svar #2
03. august 2014 af Mulledyr (Slettet)
Stoffet er thallium(I)chlorid med cæsiumchlorid struktur.
Udregning af densiteten er en delopgave der kommer efter opgaven med kantlængden.
Disse oplysninger har man også til rådighed:
MTl=204,383 g/mol MCl=35,453
og så avogadros tal; NA=6,023*1023 mol-1
Svar #3
03. august 2014 af bbdk
Nåå ja. Braggs lov. Men hvorfor har du divideret med 2?
Jeg ville sige det er 1,5406Å/sin(16.5 gr) = 5,4Å
Nu snød jeg lige og regnede densiteten ud og tjekkede TlCl densitet på wiki. Det passer med at kantlængden er 5,42
Svar #4
03. august 2014 af Mulledyr (Slettet)
Det var også sådan jeg gjorde til at starte med. Men min facitliste siger, at jeg skal dele med to.
Jeg er lidt i tvivl om, om der er fejl i facitlisten?
Og hvordan finder jeg kantlængden?
Svar #5
03. august 2014 af mathon
Betragtes en CsCl-krystal, der består af et mol cæsiumchlorid, indeholder den 2NA ioner
(gitterpunkter).
Kaldes den molære masse M og densiteten ρ, er rumfanget af ét gitterpunkt formet som en terning om
punktet lig med
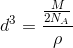
og kantlængden
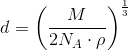
Svar #6
04. august 2014 af mathon
samt
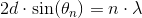 hvor n er antal atomlag
hvor n er antal atomlag
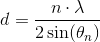
Diffraktionstrålerne- bestemt ved de forskellige værdier af n - afviger vinklen 2θ fra den direkte gennemgående stråle, der ofte kaldes centralstrålen.
For n = 1
haves
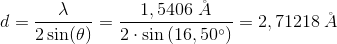
Svar #9
04. august 2014 af Mulledyr (Slettet)
Mange tak for hjælpen =D
Kan du også hjælpe mig med at finde kantlængden, a?
Skriv et svar til: Braggs lov - CsCl struktur
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.







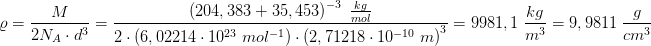
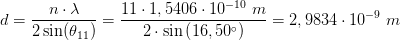
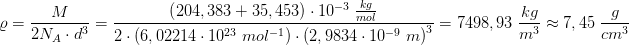
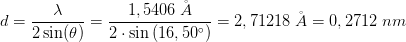
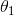 er jo ikke
er jo ikke 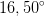 som forkert anvendt i #10.
som forkert anvendt i #10.