Matematik
Praktisk anvendelse af en potensfunktion.
Hej derude. Er der nogen der kan give et eksempel på en praktisk potensfunktion? Har ikke helt forstået det, så sidder lidt fast ved denne opgave. Håber i vil hjælpe, det ville være pænt af jer. Mvh.
Svar #1
20. maj 2016 af 102938475 (Slettet)
En potensfunktion har den generelle forskrift:
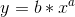
Et eksempel kunne være: 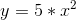
Håber, at det var det der blev spurgt om :)
Svar #2
20. maj 2016 af Christianku (Slettet)
Hov, tror måske jeg formulerede det forkert. Det skal være et eksempel på praktisk anvendelse af en potensfunktion. Altså, brug af af en potensfunktion i dagligdagen
Svar #3
20. maj 2016 af Sfeldt (Slettet)
Et praktisk eksempel på en potensfunktion kunne være
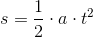
strækning for en accelererende bevægelse. Hvis a f.eks. er 2 m/s^2 så ville strækningen være
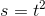
eller
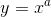
Svar #4
21. maj 2016 af flem1739 (Slettet)
Hej
Et andet praktisk eksempel på en potensvækstfunktion er sammenhængen mellem vandstanden i en balje med skrå sider (baljen har dermed stigende tværsnitsareal med voksende vandstand) og tiden t, når baljen tilføres en fast mængde vand pr. tidsenhed.
Hvis baljen er en kegle, der står på hovedet, er h(t) = k * t (1/3)
hvor konstanten k = (3 * s * tan2(v) / pi) (1/3), s er den tilførte vandmængde (Liter pr. tidsenhed) og v er vinklen, som keglens sider danner med vandret.
mvh Flemming
Svar #5
21. maj 2016 af Eksperimentalfysikeren
Hvis man designer programmer til behandling af store datamængder, er det interessant at vide, hvor stort regnearbejde, der kræves for at løse opgaven. F. eks. Hvor mange regneoperationer skal der til at løse n ligninger med n ubekendte? Man er især interesseret i, hvordan antallet af regneoperationer stiger, når n vokser. Der er forskellige metoder til ligningsløsning. Så vidt jeg husker bruger én af metoderne k1*n3 regneoperationer, mens en anden bruger k2*n2. regneoperationer.
Rene potensfunktioner er ikke så hyppige, men når man samler flere sammen til et polynomium, f.eks. a0+a1x+a2x2+a3x3+...+anxn, bliver anvendelsesmulighederne meget større. Hvis man vil kende funktionsværdien for sin(x), kan man benytte et polynomium til at tilnærme værdien. Når en lige jernbanestrækning skal gå over i et sving, kan man ikke bare starte med en cirkelbue. Det vil give et ryk i toget og få det til at vælte. Derfor bruger man en overgangsbue, som kan være beskrevet ved et 4.grads polynomium. Når man skal regne på strålegangen igennem en serie linser, der tilsammen danner et fotografisk objektiv, bruger man polynomier i flere variable. I gamle dage nøjedes man med 3. grad, da man skulle regne det hele i hånden. I dag foregår det med specielle programmer på computer og man vælger polynomier af højere grad.
Svar #6
21. maj 2016 af peter lind
I vejdirektoratet anvender man potensfunktioner til at modellere trafikuheld. Variabel er trafikken. modellerne er fordelt på forskelleige vejtyper og kryds for eks. motorvej, motortrafikvej, landevej o.s.v.
Skriv et svar til: Praktisk anvendelse af en potensfunktion.
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.








