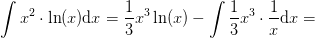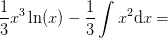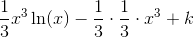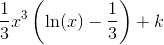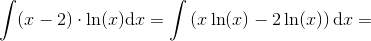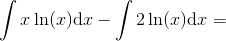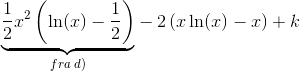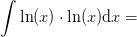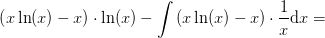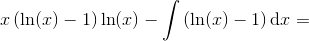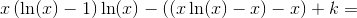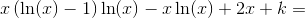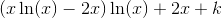Matematik

Partiel integration eller delvis integration

05. september 2016 af CamillaKMortesen (Slettet) - Niveau: A-niveau

Hej

Jeg har nogle problemer med nogle lektier. Jeg skal bestemme integralet i opgave c, e og f, som kan ses på billedet. Jeg kan godt finde resultaterne ved brug af Maple, men jeg skal vide, hvordan man gør ¨i hånden¨.

På forhånd tak

Vedhæftet fil: integration.jpg

Brugbart svar (0)

Svar #1
05. september 2016 af mathon

Brugbart svar (0)

Svar #2
05. september 2016 af VandalS

Partiel integration benyttes med fordel på integraler, hvor integranden i det nye integral bliver "simplere" end i det originale integral. Dette gælder f.eks. produkter af funktioner hvor den ene funktion er et polynomium, da denne ved gentagen partiel integration udgår idet graden af polynomiet reduceres med 1 for hver gang der udføres partiel integration.

Som et vejledende eksempel er her opgave c:

Vi skal ved brug af partiel integration beregne integralet

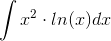$\int{x^2 \cdot ln(x)dx}$ .

Vi ønsker at den nye integrand skal være simplere end den nuværende. Hvis vi sætter 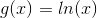g(x)=ln(x) falder polynomiet én grad i det nye integral, men dette opvejes af den ekstra faktor 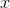der opstår ved at integrere ln(x) .

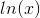Vi sætter derfor 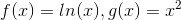f(x)=ln(x), g(x)=x^2 , hvorved partiel integration giver os at

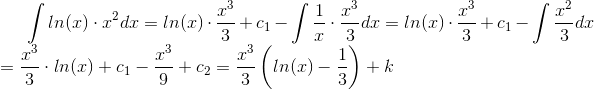
$\int{ln(x) \cdot x^2 dx} = ln(x)\cdot \frac{x^3}{3} + c_1- \int{\frac{1}{x} \cdot \frac{x^3}{3}dx} = ln(x) \cdot \frac{x^3}{3} + c_1 - \int{\frac{x^2}{3}dx} \\ = \frac{x^3}{3} \cdot ln(x) + c_1 - \frac{x^3}{9} +c_2 = \frac{x^3}{3} \left( ln(x) - \frac{1}{3} \right ) + k$

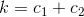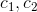hvor k=c_1 + c_2 og c_1,c_2 er arbitrære integrationskonstanter.

Brugbart svar (0)

Svar #3
05. september 2016 af mathon

c)
$\int x^2\cdot \ln(x)\mathrm{d}x=\frac{1}{3}x^3\ln(x)-\int \frac{1}{3}x^3\cdot \frac{1}{x}\mathrm{d}x=$

$\frac{1}{3}x^3\ln(x)-\frac{1}{3}\int x^2\mathrm{d}x=$

$\frac{1}{3}x^3\ln(x)-\frac{1}{3}\cdot \frac{1}{3}\cdot x^3+k$

$\frac{1}{3}x^3\left (\ln(x)-\frac{1}{3} \right )+k$

Brugbart svar (0)

Svar #4
05. september 2016 af mathon

e)
$\int (x-2)\cdot \ln(x)\mathrm{d}x=\int \left (x\ln(x)-2\ln(x) \right )\mathrm{d}x=$

$\int x\ln(x)\mathrm{d}x-\int 2\ln(x)\mathrm{d}x=$

$\underset{fra\; d)}{\underbrace{\frac{1}{2}x^2\left ( \ln(x)-\frac{1}{2} \right )}}-2\left ( x\ln(x)-x \right )+k$

Brugbart svar (0)

Svar #5
05. september 2016 af mathon

f)
$\int \ln(x)\cdot \ln(x)\mathrm{d}x=$

$\left ( x\ln(x)-x \right )\cdot \ln(x)-\int \left ( x\ln(x)-x \right )\cdot \frac{1}{x}\mathrm{d}x=$
$x\left ( \ln(x)-1 \right )\ln(x)-\int \left (\ln(x)-1 \right )\mathrm{d}x=$

$x\left ( \ln(x)-1 \right )\ln(x)-\left (\left ( x\ln(x)-x \right )-x \right )+k=$

$x\left ( \ln(x)-1 \right )\ln(x)-x\ln(x)+2x+k=$

$\left (x\ln(x)-x-x \right )\ln(x)+2x+k$

$\left (x\ln(x)-2x \right )\ln(x)+2x+k$

Skriv et svar til: Partiel integration eller delvis integration

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.