Matematik
Rumgeometri - Vektorer
Hej alle,
Jeg har en opgave ( se vedhæftet fil)
Skal jeg ikke starte med at beregne værdien af t, ved at sætte det lig med 2^sqrt(3). Men jeg skal vælg anvende formlen for krydsproduktet:
a x b/a*b
hvoraf jeg sætter det lig med 2^sqrt(3) og beregner værdien for t, men jeg skal vel sætte vektorerne under en kvadratrod og derefter dividere med kvadratroden af den ene vektorer ganget med den anden vektor, og når jeg har fundet t, skal jeg vel bare erstatte resultatet med t?
vektor a = (1,2,3) vektor b=(1,t,t+1)
Tak på forhånd!
Svar #3
23. august 2017 af H3h3 (Slettet)
#2
Jeg krydser vektorene med hinanden og sætter det lig med 2^sqrt(3)?
Svar #9
23. august 2017 af H3h3 (Slettet)
#4
Du krydser først vektorene med hinanden, og derefter tager du så kvadratroden? Men hvad har de 1/2, så med det her at gøre?
Svar #11
23. august 2017 af H3h3 (Slettet)
#10det vides ikke
om der meneseller
Hvad mener du? Det står i opgaven #1
Skriv et svar til: Rumgeometri - Vektorer
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.





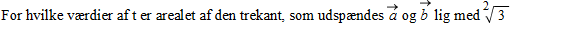
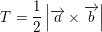
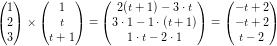
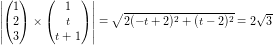
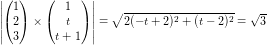
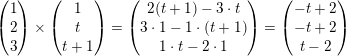
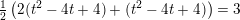
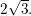
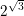 harmonerer ikke med
harmonerer ikke med