Fysik

strømstyrken

11. oktober 2018 af Nanna34 - Niveau: B-niveau

jeg ved godt at I i en serie forbindelse er det samme, mens i en parallele forbindelse, deler sig. men jeg kan ikke helt finde ud af det, gerne hjælp med forklaring plz.

Vedhæftet fil: Screen Shot 2018-10-11 at 20.16.14.png

Brugbart svar (1)

Svar #1
11. oktober 2018 af PeterValberg

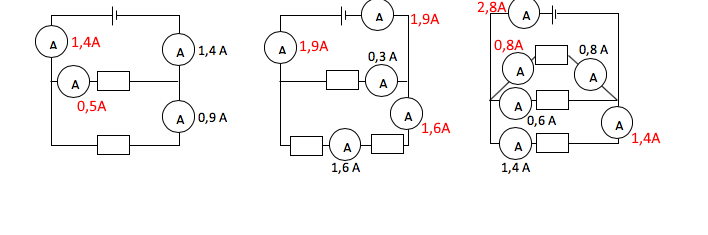
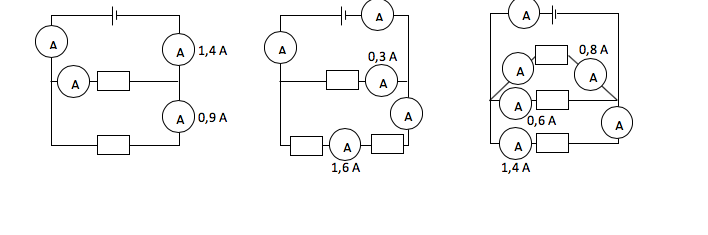
Jeg indsætter lige dit billede, det gør det nemmere at hjælpe:

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #2
11. oktober 2018 af PeterValberg

Kirchhoff's lov om strømdeling ("strømloven") siger,
at summen af de strømme, der løber til et knudepunkt
er lig med summen af de strømme, der løber derfra.

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #3
11. oktober 2018 af PeterValberg

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Unavngivet.png

Svar #4
11. oktober 2018 af Nanna34

#3
sa

mange tak:))))) men altså jeg er meget forvirret, skal man ikke bruge sin viden fra serie og parallel forbindelse lov?

Brugbart svar (1)

Svar #5
11. oktober 2018 af PeterValberg

Disse opgaver kan løses udelukkende ved at kende til
Kirchhoff's lov om strømdeling ved knudepunkter

- - -

mvh.

Peter Valberg
(YouTube)

Svar #6
11. oktober 2018 af Nanna34

#5
Disse opgaver kan løses udelukkende ved at kende til
Kirchhoff's lov om strømdeling ved knudepunkter

hmm, jamen hvornår kan jeg ved hvilket lov skal jeg bruge, kan du vise mig flere eksempler, jeg har en test imorgen :(

Brugbart svar (0)

Svar #7
11. oktober 2018 af ringstedLC

Hvis du med "... hvilket lov skal jeg bruge" mener Kirchoff's- eller Ohm' s lov, er svaret Kirchoff's lov, fordi det kun er strømmene, der oplyses. Ohm's lov kræver U og R for at I kan beregnes.

Svar #8
12. oktober 2018 af Nanna34

#2
Kirchhoff's lov om strømdeling ("strømloven") siger,
at summen af de strømme, der løber til et knudepunkt
er lig med summen af de strømme, der løber derfra.
Ka du sætte tal på? Summen af hvilke to ?

Brugbart svar (0)

Svar #9
12. oktober 2018 af PeterValberg

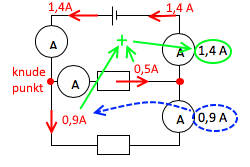
Her er et eksempel fra din aktuelle opgave:

- - -

mvh.

Peter Valberg
(YouTube)

Vedhæftet fil:Unavngivet.png

Svar #10
12. oktober 2018 af Nanna34

#9
Her er et eksempel fra din aktuelle opgave:

Jeg fårstået stadig væk ik:((

Brugbart svar (0)

Svar #11
13. oktober 2018 af ringstedLC

Et knudepunkt er et punkt på en af forbindelserne i kredsløbet, hvorfra der er mere end to tilledninger.

Strømmen I_L løber fra spændingskilden gennem A-meteret til det venstre knudepunkt i din opgave.

Kirchoff's lov siger omskrevet, at strømmen ikke kan forsvinde (- ud af kredsløbet). Den I_L, der løber til knudepunktet, må derfor være summen af de strømme, I₁ og I₂, der løber væk fra knudepunktet.

$\begin{align*} I_{2} &=0.9\;A\\ I_{L} &= {\color{Red} 1.4\;A}=I_{1}+I_{2}\Downarrow\\ I_{1} &=1.4\;A-I_{2}\Downarrow\\ I_{1} &=1.4\;A-0.9\;A\Downarrow\\ I_{1} &=0.5\;A \end{align*}$

I det højre knudepunkt mødes I₁ og I₂ og bliver til I_L igen.

Det er derfor, at vi generelt kan regne på serie- og parallelkoblinger som det gøres.

Brugbart svar (0)

Svar #12
13. oktober 2018 af ringstedLC

Forestil dig kredsløbet opgivet uden strømmen I₂, men med U = 0.9 V, den nederste modstand R₂ = 1 Ω og spørgsmålet: Beregn R₁

Da modstandene er koblet i parallel, beregnes R₁ ved:

$\begin{align*} \frac{1}{R_{L}} &=\frac{1}{R_{1}}+\frac{1}{R_{2}}\Downarrow\\ \frac{1}{R_{1}} &=\frac{1}{R_{L}}-\frac{1}{R_{2}}\Downarrow\\ \frac{1}{R_{1}} &=\frac{1\cdot R_{2}}{R_{L}\cdot R_{2}} -\frac{1\cdot R_{L}}{R_{2}\cdot R_{L}}\Downarrow\\ \frac{1}{R_{1}} &=\frac{R_{2}-R_{L}}{R_{2}\cdot R_{L}}\Downarrow\\ R_{1}\cdot \left(R_{2}-R_{L}\right) & =1\cdot R_{2}\cdot R_{L}\Downarrow\\ R_{1} &=\frac{R_{2}\cdot R_{L}}{\left(R_{2}-R_{L}\right)} \end{align*}$

Ved indsætning i Ohm's lov fås R_L:

$\begin{align*} U &=0.9\;V\;,\;I_{L}=1.4\;A\\ U &=I_{L}\cdot R_{L}\Downarrow\\ R_{L} &= \frac{U}{I_{L}}\Downarrow\\ R_{L} &= \frac{0.9\;V}{1.4\;A}\Downarrow\\ R_{L} &= 0.643\;\Omega \end{align*}$

Ved indsætning fås R₁:

$\begin{align*} R_{1} &=\frac{R_{2}\cdot R_{L}}{\left(R_{2}-R_{L}\right)}\;,\;R_{2}=1\;\Omega\;,\;R_{L}=0.643\;\Omega\\ R_{1} &=\frac{1\cdot 0.643}{1-0.643}\;\frac{\Omega^2}{\Omega}\Downarrow\\ R_{1} &=1.8\;\Omega \end{align*}$

Skriv et svar til: strømstyrken

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.