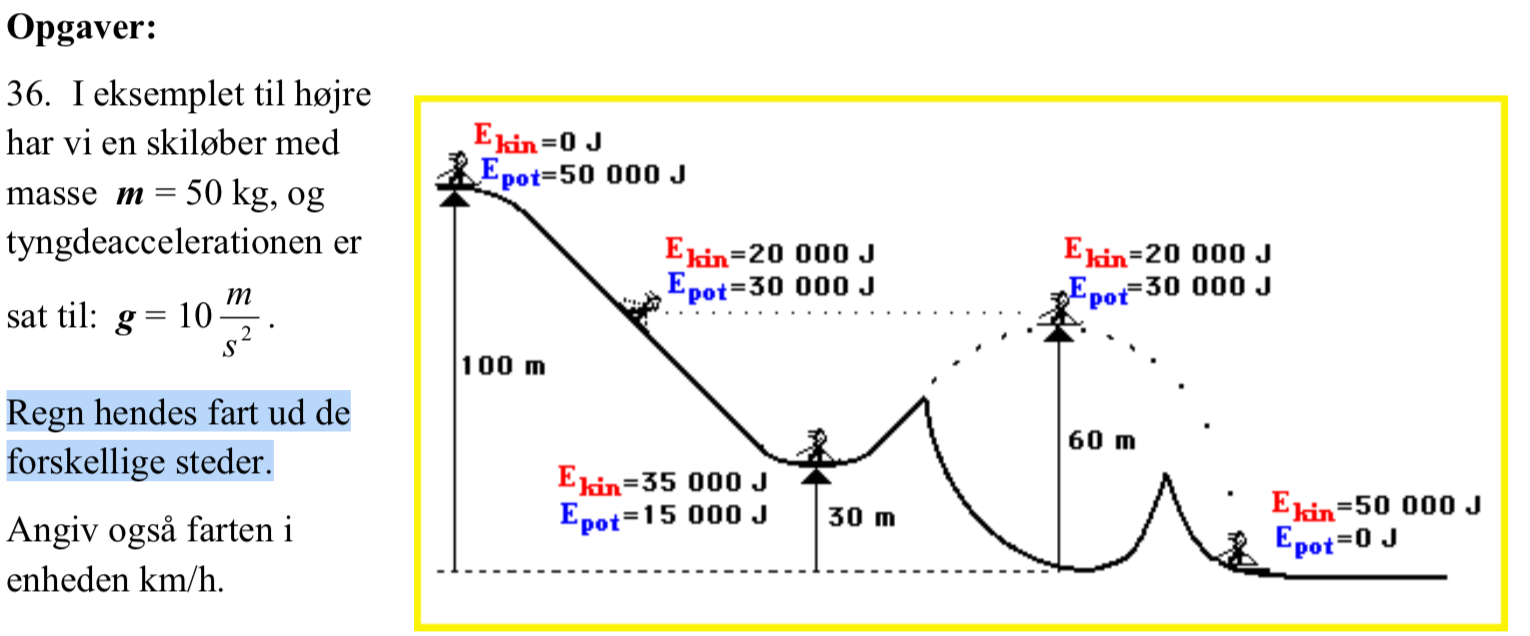
Fysik

En skiløber med massen m, og tyngdeacceleration g

14. februar 2019 af Christensen5 (Slettet) - Niveau: C-niveau

Hej!

Følgende opgave forvolder lidt problem, fordi formlen for Mekanisk energi er E_mek = E_pot + E_{Kin. Men med følgende formel, finder man jo ikke hastigheden? Hvordan skal en formel stilles op for denne type opgave?}

Tak på forhånd!

Vedhæftet fil: Screenshot 2019-02-14 at 07.44.22.png

Brugbart svar (0)

Svar #1
14. februar 2019 af janhaa

du vet:

$E_k=0,5mv^2\\ E_p=mgh$

Brugbart svar (0)

Svar #2
14. februar 2019 af mathon

Brugbart svar (0)

Svar #3
14. februar 2019 af mathon

Den mekaniske energi er konstant.

$\small \tfrac{1}{2}\cdot m\cdot v^2+m\cdot g\cdot h=5\cdot 10^4\; J$

$\small \tfrac{1}{2}\cdot v^2+ g\cdot h=\frac{5\cdot 10^4\; \tfrac{kg\cdot m^2}{s^2}}{50\; kg}=1000\; \tfrac{m^2}{s^2}$

$\small \tfrac{1}{2}\cdot v^2+ g\cdot h=1000\; \tfrac{m^2}{s^2}$

$\small v^2+ 2\cdot g\cdot h=2000\; \tfrac{m^2}{s^2}$

$\small \small v(h)= \sqrt{\left (2000\; \tfrac{m^2}{s^2} \right )-\left (20\; \tfrac{m}{s^2} \right )\cdot h}$

Svar #4
14. februar 2019 af Christensen5 (Slettet)

Tak for svar!

Jeg er bare lidt i tvivl om det sidste punkt. Hvor kommer (-20 m/ S²). fra?

Brugbart svar (0)

Svar #5
14. februar 2019 af ringstedLC

$\begin{align*} v^2+2gh &= 2000\;\left ( \frac{m^2}{s^2}\right ) \\ v^2 &= 2000-2gh \\ v(h) &= \sqrt{2000-2\cdot 10\cdot h}\;\left ( \sqrt{\frac{m^2}{s^2}}=\frac{m}{s} \right ) \\ \end{align*}$

Brugbart svar (1)

Svar #6
14. februar 2019 af Eksperimentalfysikeren

Det er ret enkelt at regne ud. Et eksempel: Jeg nummererer positionerne, så startstedet er nummer 0, ned ad første bakke 1, i bunden 2 osv. Vi ser på 1. Her står der på figuren, at den kinetiske energi er 20 000J. Massen er 50kg. Så har vi:

20000J = ½*50kg*v²

Gang med 2 og divider med 50kg, så har vi:

$\frac{20 000J*2}{50kg} =v^{2} = 800(\frac{m}{s})^{2}$

Så

$v = \sqrt{800}\frac{m}{s}$

Der er ingen grund til at regne den potentielle energi med i foretagendet, for den er allerede trukket fra på figuren.

Brugbart svar (0)

Svar #7
16. februar 2019 af mathon

$\small \begin{array}{rclcrcl} v&=&\sqrt{4\cdot \{E_{kin}\}\cdot 10^{-2}}\; \tfrac{m}{s}\\\\ v&=&\sqrt{4\cdot \{0\}\cdot 10^{-2}}\; \tfrac{m}{s}&=&0\\\\ v&=&\sqrt{4\cdot \{2\cdot 10^{4}\}\cdot 10^{-2}}\; \tfrac{m}{s}&=&28.28\; \tfrac{m}{s}\\\\ v&=&\sqrt{4\cdot \{3.5\cdot 10^{4}\}\cdot 10^{-2}}\; \tfrac{m}{s}&=&37.42\; \tfrac{m}{s}\\\\ v&=&\sqrt{4\cdot \{5\cdot 10^{4}\}\cdot 10^{-2}}\; \tfrac{m}{s}&=&44.72\; \tfrac{m}{s} \end{array}$

Brugbart svar (0)

Svar #8
16. februar 2019 af mathon

detaljer:
$\small v=\sqrt{\frac{2E_{kin}}{m}}=\sqrt{\frac{2\{E_{kin}\}\cdot \tfrac{kg\cdot m^2}{s^2}}{50\; kg}}=\sqrt{\frac{4\{E_{kin}\}}{100}}\; \tfrac{m}{s}=\sqrt{4\cdot \{E_{kin}\}\cdot 10^{-2}}\; \tfrac{m}{s}$

Skriv et svar til: En skiløber med massen m, og tyngdeacceleration g

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.