Matematik

Jeg ved ikke engang hvad type opgave det er

20. marts 2019 af KennethLarsens - Niveau: B-niveau

Jeg er simelthen helt fuldstændig lost: så jeg vedhæfte bare opgaven og håber i kan hjælpe mig:

Vedhæftet fil: Skærmbillede 2019-03-20 kl. 20.16.54.png

Brugbart svar (0)

Svar #1
20. marts 2019 af peter lind

Svar #2
20. marts 2019 af KennethLarsens

Nogen der kan hjælpe lige umidelbart, jeg er simpelthen helt lost med denne opgave

Brugbart svar (0)

Svar #3
20. marts 2019 af peter lind

Når den indeholder 1000 cm³ er højden til væskeoverfladen areal*højde =1000cm³. Da arealet er x² og der ska lægges 2 cm til for du x²*(h-2)=1000

Overffladearelet = x² +4*x*h

Brugbart svar (0)

Svar #4
20. marts 2019 af mathon

$\small O(x)=x^2+8x+\frac{4000}{x}\qquad 0<x<30$
minimal overflade
kræver bl.a.
$\small O{\, }'(x)=2x+8-\frac{4000}{x^2}=0$

$\small x^3+4x^2-2000=0\qquad 0<x<30$

$\small x=11.40$

Svar #5
20. marts 2019 af KennethLarsens

#4
$\small O(x)=x^2+8x+\frac{4000}{x}\qquad 0<x<30$
minimal overflade
kræver bl.a.
$\small O{\, }'(x)=2x+8-\frac{4000}{x^2}=0$

$\small x^3+4x^2-2000=0\qquad 0<x<30$

$\small x=11.40$

Er svar 3 så forkert, eller? jeg er meget forvirret for at være ærlig, og hvor kommer x^2 fra ved O' under de 4000?

Brugbart svar (0)

Svar #6
20. marts 2019 af mathon

#3 er ikke rigtig.
$\small \textup{overfladearealet \ae ndres ikke, fordi beholderen ikke er fyldt helt op med v\ae ske.}$

Brugbart svar (0)

Svar #7
20. marts 2019 af AMelev

#0 Det er en typisk optimeringsopgave, hvor der indgår to variable og en oplysning fx om rumfang, så man kan udtrykke den ene variabel ved den anden. Derudfra skal man så bestemme udtrykket for noget andet fx overfladeareal, som så skal optimeres (minimeres/maksimeres).

Jf. #3 Løs ligningen x²·(h - 2) = 1000 mht. h (udtrykt ved x).
Det bruger du så til at bestemme overfladearealet (se #3)

Derefter bestemmer du min for O(x) på sædvanlig vis.

Brugbart svar (0)

Svar #8
20. marts 2019 af AMelev

#5 Svar 3 er rigtig. Hvis du arbejder med det som skrevet i #3 og #7 finder du ud af at udtrykket for O(x) passer.
#4 vedrører minimeringen i sp. b). Til O'(x) kan du bare bruge dit CAS-værktøj. Så får du måske ikke lige det samme udtryk, men forskellen på dit og det i #4 skulle gerne være 0.

Brugbart svar (0)

Svar #9
20. marts 2019 af Soeffi

#0. Ti-Nspire:

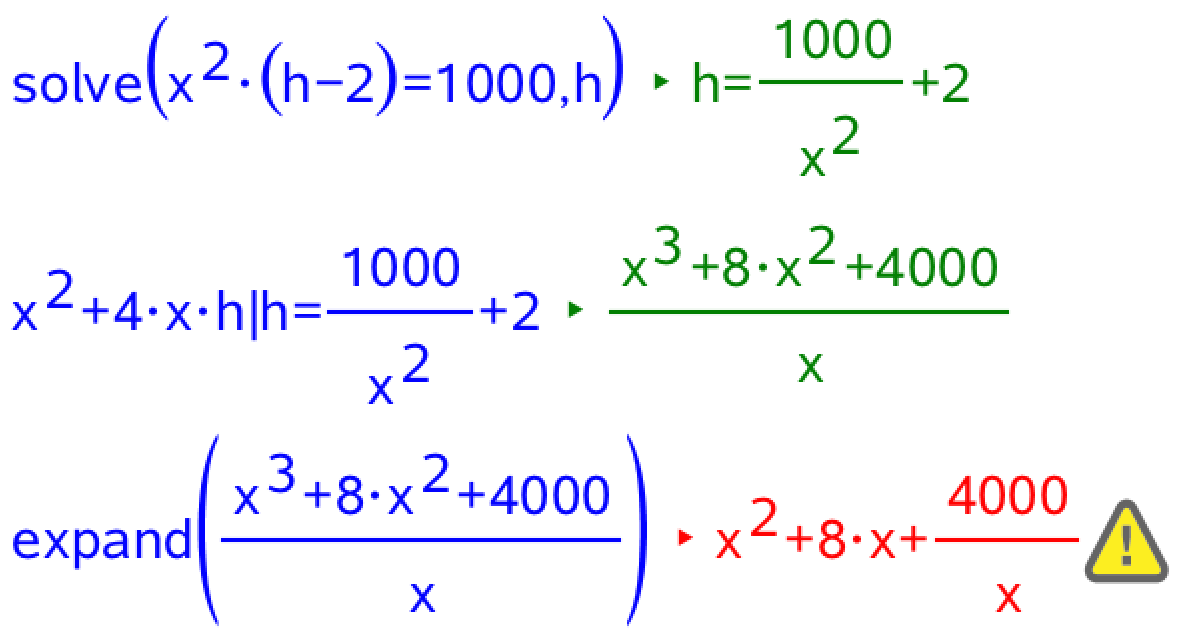
Vedhæftet fil:Skærmbillede 2019-03-20 kl. 21.38.27.png

Skriv et svar til: Jeg ved ikke engang hvad type opgave det er

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.