Objekts volumen i 3D

Brug hjælpepunktet F(0; 0; 0). Find volumen af polygonet AFCBDE, og gang dette med 6. Husk at D(0; 0; 3).

Hvorfor skal det ganges med 6? Er polygonet afcbde ikke Grundfladen, og derefter kan jeg bare gnge med højdn for at få pyramidestubbens volumen?

Det kommer an på hvordan du opfatter polygonet. Hvad har du fået s ligning til? Du kan eventuelt bruge det til at finde volumen.

Hvordan findet jeg volumen vha. den? har vedhæftet den

Sådan her:

Det er det bestemte integral som finder arealet mellem to kurver som funktion af x, hvorefter man finder det bestemte areal af dette areal som funktion af y. Dette resulterer i volumnet af én 6-del af toiletbygning, cirka 6.6655

Hvordan ville jeg opskrive det i maple? Tror ik man kan skrive dy....

sådan

Hvorfor skal den løses for z? 

Og er det volumen for pyramidestubben? hvad med pyramiden

Det der tager jo begge flader med i regnestykket (så det er både pyramide og pyramidestub). Løsningen her er halv, man skal lige have styr på hvor man tager integralet. Volumnet her er for stort, da det kun bør være omkring 3. Vent lige lidt :)

Metoden bør dog godt kunne bruges.

Vi skal først tage det bestemte dobbeltintegral for at finde volumen under  i det interval hvor og derefter for differensfunktioner. Kommer med et resultat senere.

Beklager. Jeg har nu løst opgaven gennem dobbeltintegraler. Løsningen involverer to gaffeludtryk, men giver heldigvis det korekte resultat.

Må jeg se din løsning, evt. med notation? Så jeg forstår hvad der sker? :D

Vi behøver ikke integralregning til bestemmelse af pyramidestubbens og pyramidens rumfang.
De er begge regulære legemer, hvortil der findes færdige formler.
Pyramidestubbens bund er seks gange arealet af en ligesidet trekant med siden 1,3
  og
pyramidestubbens top er seks gange arealet af en ligesidet trekant med siden 1,8 .
Højden er 2,5
For pyramiden, taget på bygningen, har vi den velkendte rumfangsformel.
Koordinaterne behøves ikke til rumfangsbestemmelserne, når vi kender |AC| og |BE| og de to's højder.

Hey Sune - kan du evt uddybe. Og arealet er vel grundfladen, ik?

Definer først dine to funktioner, som er ligningerne for de to planer og (givet i opgaven).

Vi definerer herefter to stykvise funktioner, som indeholder de intervaller vi ønsker. Vi skal finde de tre betingelser eq1, eq2 og eq3.

eq1 er der hvor og skærer hinanden løst for y (svarer til ligningen for den linje BE danner): .

eq2 er ligningen for den linje som AC danner: .

eq3 er ligningen for den linje som origo og C danner:

Vi vil gerne have at de er 0 når vores betingelser ikke er opfyldt, da vi tager integralet over et rektangulært domæne i .

Vi kan sætte det ind i Maple.

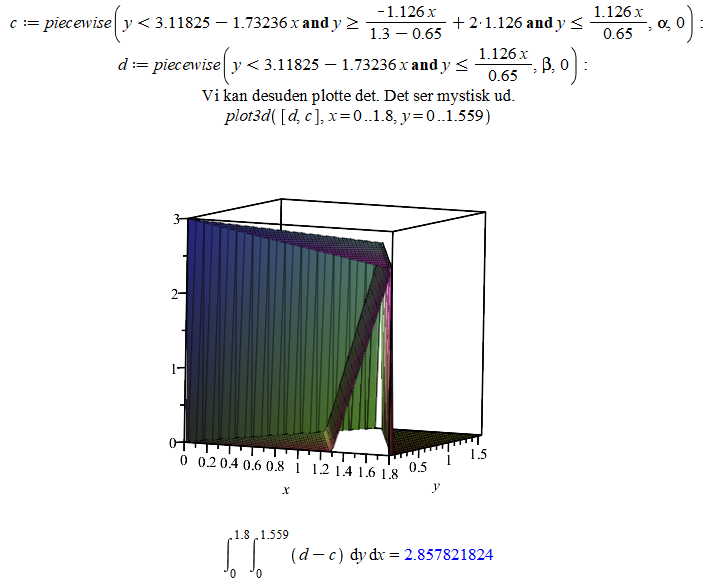
Resultatet er egentlig ret tæt på det jeg forventede. Jeg har tidligere approksimeret det til at være 2.85 ved at tage gennemsnittet af to prismer i Geogebra. Resultatet er det rigtige, og det passer intuitivt sammen. Vi kan nu gange dette med 6 for at opnå det totale volumen af toiletbygningen.

#14

Vi behøver ikke integralregning til bestemmelse af pyramidestubbens og pyramidens rumfang.

Nej, vi kan godt løse det geometrisk, men der bliver nærmest lagt op til at løse det med analytisk gennem integraler og funktioner. I forhold til niveauet er det klart at hoppe uden for pensum (man beregner kun volumner af omdrejningslegemer vha. integraler på htx).

Og så er det jo altid sjovt at lære noget nyt om infinitesimalregning.

Grundfladens areal findes ved at opdele den i 6 ens trekanter. De bliver ligesidede, fordi de 360 grader inde i midten deles i 6 lige store vikler, altså 60 grader til hver, og de liniestykker, der går ud til hjørnerne fra midten er lige lange. Arealet af en enkelt trekant kan findes ved først at finde højden i trekanten. I en ligesidet trekant gælder:

Det indsættes i formlen for trekantens areal. Grundlinien er opgivet som AC i opgaven. Tilsvarende med den anden grundflade oppe under taget. Dens kantlængde er også opgivet i opgaven. Derefter slår du formlen for rumfanget af en pyramidestub op. Det er den af formlerne, hvor man går ud fra grundfladearealerne.

Husk at finde rumfanget af pyramidetaget.

# 17
Dobbeltintegraler skal læres (og forstås) fra bunden. Det er, aktuelt, ikke-niveausvarende.
__________
# 18                 

#19 om #18 Korrekt, Tak for rettelsen.