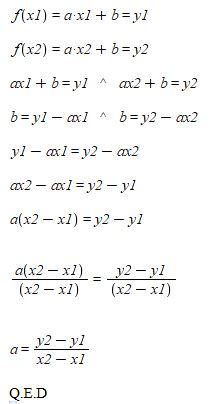Matematik

Bevis for formlerne a og b

03. november 2019 af joseflahlou (Slettet) - Niveau: B-niveau

Jeg skal bevise, hvordan man beregner regneforskriften for en linære funktion, når man kender 2 punkter fra en funktions graf. Og jeg ønsker at for dette uddybet fra linje til linje, så jeg bedre kan forstå, hvad der sker. Tjek billedet for at se, hvad jeg snakker om.

Vedhæftet fil: a og b.JPG

Brugbart svar (0)

Svar #1
03. november 2019 af Kap1D

Hvor går det galt med forståelsen? Er det et specifik trin i regnerækken eller er det ideen med beviset?

Brugbart svar (0)

Svar #2
03. november 2019 af peter lind

Brugbart svar (1)

Svar #3
03. november 2019 af Mathias7878

Givet to punkter

$(x_1,y_1) \ og \ (x_2,y_2)$

der ligger på den rette linje med forskriften

$y = ax+b$

kan man opstille to ligninger

$y_2 = ax_2+b \ samt \ y_1=ax_1+b$

og disse kan man trække fra hinanden, dvs

$y_2-y_1 = ax_2+b-(ax_1+b)$

hvilket reduceres til

$y_2-y_1 = ax_2-ax_1$

og det bemærkes, at a indgår i begge led, dvs. vi kan sætte a uden for en parentes

$y_2-y_1 = a\cdot (x_2-x_1)$

og der divideres så med x_2-x_1 på begge sider, dvs

$a = \frac{y_2-y_1}{x_2-x_1}$

og formlen for b kan man bevise ved at isolere b i en af formlerne.

- - -

Svar #4
03. november 2019 af joseflahlou (Slettet)

#1
Hvor går det galt med forståelsen? Er det et specifik trin i regnerækken eller er det ideen med beviset?

Jeg forstår ikke trinene i regnerækken.

Brugbart svar (0)

Svar #5
03. november 2019 af Mathias7878

Giver #3 så mening?

- - -

Svar #6
03. november 2019 af joseflahlou (Slettet)

#3
Givet to punkter

$(x_1,y_1) \ og \ (x_2,y_2)$

der ligger på den rette linje med forskriften

   $y = ax+b$

kan man opstille to ligninger

   $y_2 = ax_2+b \ samt \ y_1=ax_1+b$

og disse kan man trække fra hinanden, dvs

   $y_2-y_1 = ax_2+b-(ax_1+b)$

hvilket reduceres til

   $y_2-y_1 = ax_2-ax_1$

og det bemærkes, at a indgår i begge led, dvs. vi kan sætte a uden for en parentes

$y_2-y_1 = a\cdot (x_2-x_1)$

og der divideres så med x_2-x_1 på begge sider, dvs

   $a = \frac{y_2-y_1}{x_2-x_1}$

og formlen for b kan man bevise ved at isolere b i en af formlerne.

Kan du fortælle, hvorfor man kan opstille de to ligninger?

Brugbart svar (0)

Svar #7
03. november 2019 af Mathias7878

Fordi de to punkter ligger på den rette linje med formen y = ax+b, så indsætter du dem bare deri.

- - -

Skriv et svar til: Bevis for formlerne a og b

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.