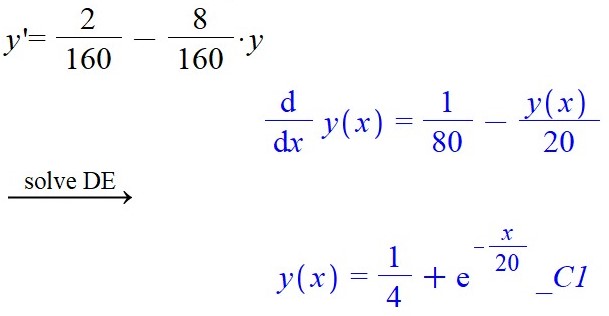Matematik

Hvad sker der her?

12. november 2019 af lol1010 - Niveau: A-niveau

Hvad gøre man her?

differentere man eller integerer?

Vedhæftet fil: SharedScreenshot.jpg

Brugbart svar (1)

Svar #1
12. november 2019 af PeterValberg

Det er en differentialligning
prøv at se video nr. 6 på denne videoliste < LINK >

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (1)

Svar #2
12. november 2019 af oppenede

y(x) isoleres

Svar #3
12. november 2019 af lol1010

Tak for det :)

Brugbart svar (0)

Svar #4
12. november 2019 af AMelev

Det, der sker, er, at differentialligningen løses med CAS (DE står nok for Differential Equation).

Hvis du selv skulle løse den, skulle du bruge separation af variable efter lige at have omskrevet højresiden.
For $y\neq \frac{1}{4}$ gælder, at $\frac{\mathrm{dy} }{\mathrm{d} x}=\frac{1}{20}\cdot (\frac{1}{4}-y)\Leftrightarrow$
$\int \frac{1 }{\frac{1}{4}-y}dy=\int \frac{1}{20}dx\Leftrightarrow -ln|\frac{1}{4}-y|=\frac{1}{20}\cdot x+k\Leftrightarrow$ $|\frac{1}{4}-y|=e^{-\frac{1}{20}\cdot x+k}\Leftrightarrow$

$\frac{1}{4}-y=\pm e^{-\frac{x}{20}}\cdot e^k\Leftrightarrow \frac{1}{4}\mp e^k\cdot e^{-\frac{x}{20}}=y\Leftrightarrow y=\frac{1}{4}+c \cdot e^{-\frac{x}{20}}, \: \: c=\mp e^k\neq 0$

For $y= \frac{1}{4}$ , fås $\frac{\mathrm{dy} }{\mathrm{d} x}=\frac{1}{20}\cdot (\frac{1}{4}-y) \Leftrightarrow 0=\frac{1}{20}\cdot 0, \: \textup{sandt,\: }$ så $y=\frac{1}{4}+c \cdot e^{-\frac{x}{20}}$ er også løsning for c = 0.

Skriv et svar til: Hvad sker der her?

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.