En funktion er givet ved...

Husk kun én opgave pr. tråd, ellers bliver det noget roderi, så læg opg. 8 op i en ny tråd, hvis du stadig skal have hjælp til den, når du har lavet opg. 7.</o:p>

Opg. 7
Figuren med trekanten mangler, den skal du lige uploade, hvis vi skal kunne hjælpe med selve opgaven.

Tegning af graf i Nspire:
Definer f(x) i Noteværktøjet: f(x):=1-x^2.
Åbn grafværktøjet og skriv f(x) i indtastningslinjen. Evt. skal du tilpasse vinduet fx med Vindue/Zoom>Zoom-Fit.

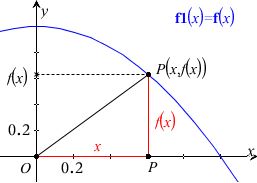
a)
Du har en retvinklet trekant, hvor du kender kateterne ud trykt ved x, så det er bare at beregne arealet
Omkredsen er OP + OQ + QP. OP bestemmes med Pythagoras.

b)
Bestem max-punkt for T(x) på sædvanlig vis ved at bestemme nulpunkter og fortegn for T'.
Bestem tilsvarende max-punkt for d(x) og sammenlign.
Du kan evt. i stedet bestemme max-punkter for T(x) og d(x) med dit grafværktøj, men husk at dokumentere, hvordan..

Jeg har skrevet det her, kan man også gøre det sådan?

#4 Ja, du har jo gjort præcis som angivet i #3.

Som jeg har skrevet i #3.

Det er det jeg ikke forstår hvordan man gør. Og jeg skal bruge TI-Nspire til det. Kan du vise hvordan man stiller det op regner det ud på TI?

OK. For det første er Nspire træls, fordi, den insisterer på små bogstaver, T(x) bliver til t(x), men du kan enten leve med det eller skrive, at du omdøbet T(x) til f(x). Jeg vil her bruge f(x)

Definer  f(x) i Noteværktøjet: f(x):=1/2*(x-x^3) (Enter)
Iflg. grafen ved du, at 0 ≤ x ≤ 1. Du kan evt. indsætte det i definitionen: f(x):=1/2*(x-x^3)|0<=x<=1 (den lodrette "betingelsesstreg" finder du under Tegn.

Metode 1
Så skal du bestemme f '(x). Nspire forstår ikke f ', så du kan kalde den fm eller df.
Her skal du bruge den femte i 3. række under skabeloner: df(x):= (x skal stå nede, da det er variablen, og f(x) oppe, da det er funktionen, der skal differentieres)
Så skal du bestemme nulpunkter for df(x), altså løse ligningen df(x) = 0: Solve(df(x)=0,x)|0<=x<=1.
Så indsætter du x-værdier på de forskellige sider af nulpunkterne i f '(x) = df(x) for at bestemme fortegnene og derudfra bestemmer du så monotoni og max/min.

Metode 2
Denne metode er legal, da definitionsmængden er begrænset til [0,1].
Åbn grafværktøjet og skriv f(x) i indtastningslinjen. Tilpas vinduet fx via Vindue/Zoom > Indstillinger for vindue.
Vælg Undersøg grafer > Maksimum og vælg nedre grænse til venstre for max-punktet og øvre grænse til højre. Så bliver max-punkt og max skrevet.

Se evt. vedhæftede.
 

Okay. Tusind tak!:)

Lige en sidste ting, hvordan bestemte du f'(3)?

Jeg har da vist ikke bestemt f '(3).
Jeg har beregnet f '(0.3) ved at indsætte 0.3 i df(x) og tilsvarende med f '(0.8).
0.3 og 0.8 er to tilfældigt valgte værdier på hver sin side af nulpunktet for f ', inden for intervallet [0,1].

Var det det, du var på jagt efter?

Ja. Så den maksimale værdi af x er: x=0,577?

Du udtrykker dig forkert, men ellers ja. Den maksimale værdi af arealet f(x) opnås ved x = 0.577.

Hvad så med omkredsen, den bølver jeg stadig med?

Og hvordan løser man opgave 8? Som jeg også har linket et billede af i toppen? Den kan jeg heller ikke finde ud af, at tegne ind og regne ud i Ti-Nspire. Kan du hjælpe?

Ny opgave - ny tråd, som jeg skrev i #1.

Har jeg lige gjort. Men hvordan fandt du den maksimale omkreds til opgave 7 b?

Jeg har ikke fundet den, for du har ikke angivet forskriften for omkredsen, men metoden er den samme som for arealet - du skal bare ændre navnet fra f(x) til d(x).

Prøv at lave en ny opgave og kopiere alt det, du har fra arealet til den nye opgave og ret så til, så det passer med omkredsen.