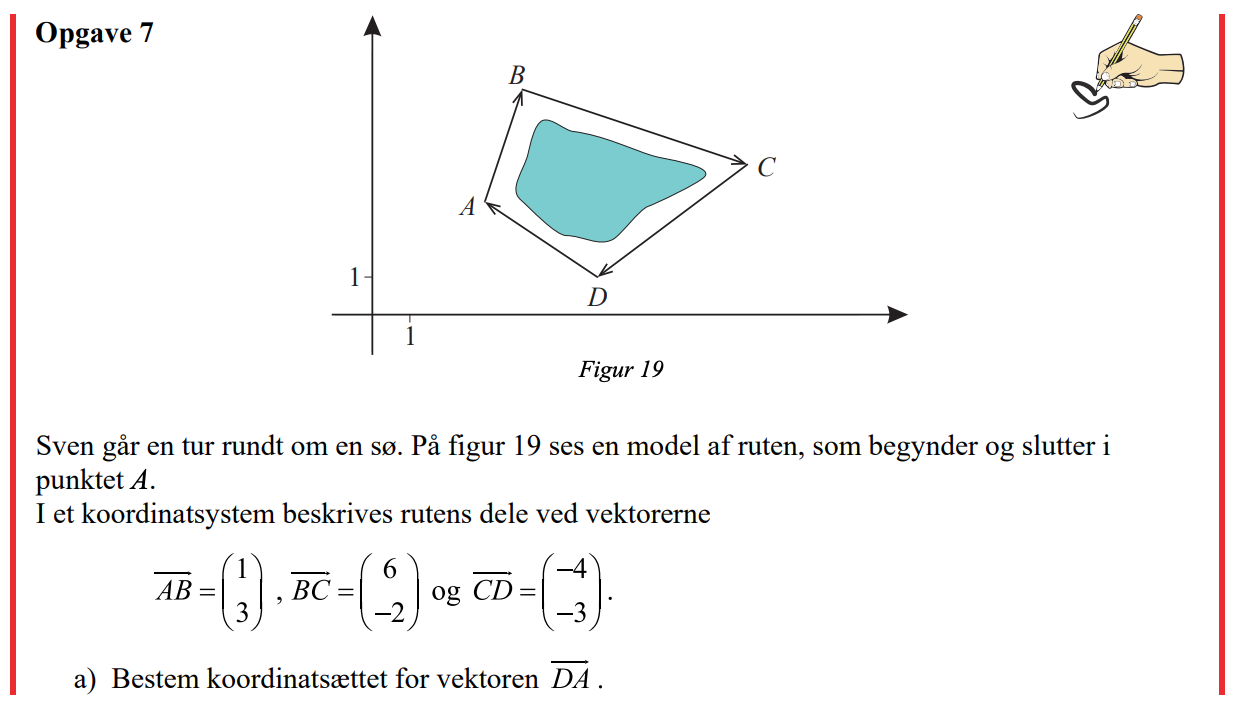
Koordinatsæt til vektoren DA

Start i A, som er (3,3).
Læg dertil vektorerne AB,BC og CD. Hvilket punkt havner du så i?
Hvilken vektor kan så bringe dig til A(3,3)?

Det ville jo så være den omvendte vektor af A+AB+BC+CD ikke?

Hvordan aflæser/beregner du at A er (3,3)?

Jeg skønner A til at være (3,3).

Men du kan også bare sige, at summen af de fire vektorer er 0-vektoren.
Så er det jo lige meget, hvor A er.

Nulvektorer er ikke en del af pensum så vidt jeg forstår, men mener du at man bare lægger summen for de 3 kendte vektorer sammen eller?

Ja.

#4: Nulvektoren er netop en del af pensum fordi den kan bruges til opgaver som denne:

Nulvektoren anvendes her, ligesom "at sætte noget lig nul" og løse en ligning med en ubekendt.

Tak!

nulvektoren virker som en lidt abstrakt idé umiddelbart, men det er vel blot et udtryk at alle vektorer hænger sammen og derfor er summen in "ikke-eksisterende" vektor? 

Når du har indset behovet for værdien "0", er det måske ikke så svært at se ideen med en vektor, der er:

Det er muligt vektorbegrebet er blevet introduceret uden megen baggrund, således som forvirringen over nulvektoren lader formode. Dertial skal blot kort siges, at opgaven viser, at man tydeligvis betragter vektorer som elementer i R^2. Det er i sig selv et vektorrum. Og et vektorrum er blot en additiv Abelsk gruppe med lidt ekstra struktur nødvendig for at definere skalarmultiplikation. Og det neutrale element ("0") i den additive gruppe er netop nulvektoren. Alle vektorrum har en nulvektor - det er et af axiomerne, der skal være opfyldt.