"Vis en metode til at afgøre om en linje er tangent til en cirkel"

En metode er at bringe linjens ligning på normalform, hvori indsættes cirklens centrums koordinater.
Da fås den vinkelrette afstand fra linjen til cirklens centrum. Er denne lig med radius, er linjen tangent til
cirklen.

Når man til mundtlig eksamen bliver bedt om at vise sådan en metode, er det så i orden kun at tegne det grafisk imens man fortæller. Altså tegne cirklen og en tangent der skærer den i netop et punkt

hvor jeg så fortæller at hvis linjen står vinkelret på radius med blot ét skæringspunkt og a*c=-1 så er den ortogonal og dermed en tangentlinje til en cirkel?

Tak for svar i de her sene timer.

Hvad betyder at bringe linjens ligning på normalform. Kan du hjælpe med et eksempel på hvordan man gør det?

Linjen  med ligningen
ax + by + c = 0
er bragt på normalformen:

Afstanden fra   til (x₀ , y₀) = 
Du skal ikke medinddrage den, hvis ikke den indgår i pensum.

#0

Se eventuelt video nr. 32 på denne videoliste < LINK >

Den formel har vi ikke arbejdet med på B niveau i nogen sammenhænge så jeg tror de vil have vi bruger en anderledes metode. Er dog stadig ikke klar over hvilken.

Vi har gennemgået at
"FInde skæringspunkt mellem cirkel og linje"
"Angive ligning til tangent når man får cirklens ligning og  et punkt P at vide"

Er det så ikke den nederste jeg skal bruge?
Se screenshot vedhæftet af nederste metode.

Til bestemmelse af afstanden fra centrum til linjen kan du bruge FS (51) side 11. Den anden udgave, der er angivet i #4, har I nok ikke haft på hfB.

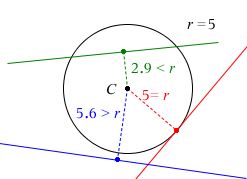
Afstanden fra punkt til linje er jo den vinkelrette (korteste) afstand, så hvis den er det samme som radius, er linjen tangent til cirklen. Hvis den er mindre end radius, skærer linjen cirklen to steder, og hvis den er større, ligger linjen helt uden for cirklen.
                                      
Og ja, det er fint at gøre rede for metoden ved at tegne og fortælle, men det kan også være en god idé at have eksempler i baghånden. 

Mange tak :) 
Jeg har valgt at løse det således udfra dit input AMelev