Matematik

Vendetangentens ligning

19. januar 2020 af MRSRN - Niveau: B-niveau

Hej..

Hvad er vendetangentens ligning?

Brugbart svar (1)

Svar #1
19. januar 2020 af peter lind

vendetangenten er en linje så den har som alle linjer ligningen y=ax+b

Svar #2
19. januar 2020 af MRSRN

hvad er så forskellen mellem almindelig tangent og vendetangent?

Brugbart svar (1)

Svar #3
19. januar 2020 af peter lind

En vendetangent er i et specielt punkt. Se https://www.studieportalen.dk/Forums/Thread.aspx?id=478797

Brugbart svar (1)

Svar #4
19. januar 2020 af StoreNord

I det punkt, hvor vendetangenten tangerer, er funktionens 2. afledede lig med 0.

Vendetangentens ligning ser ud som enhver anden anden tangentligning; det er bare punktet, der ligger et specielt sted.

Brugbart svar (0)

Svar #5
19. januar 2020 af ringstedLC

Svar #1 i linket i #3 (https://www.studieportalen.dk/Forums/Thread.aspx?id=478797#478881) er forkert og sikkert derfor undres trådstarter til linket i svar #2.

Definition: https://www.webmatematik.dk/lektioner/matematik-b/differentialregning/monotoniforhold

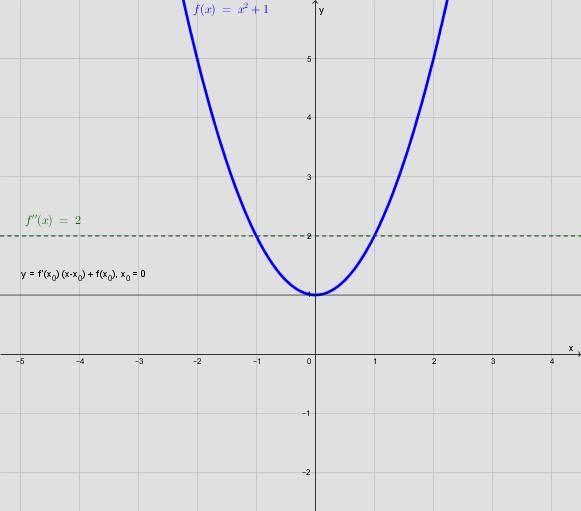
#0: Det er den samme som den for en tangent med betingelsen:

$\begin{align*} y &= f'(x_0)(x-x_0)+f(x_0)\;,\;f''(x_0)=0 \end{align*}$

Alle (alm.) tangenter (eks.):

$\begin{align*} f(x) &= x^3-3x+2 \\ f'(x)&= 3x^2-3 \\ y &= f'(x_0)(x-x_0)+f(x_0) \\ y &= (3{x_0}^2-3)(x-x_0)+f(x_0) \end{align*}$

Vendetangent:

$\begin{align*} {\color{Red} f''(x)}=(f'(x))' &=6x=0\Rightarrow x=0 \\ y &= (3{x_0}^2-3)(x-x_0)+f(x_0)\;,\;x_0=0 \\ y &= (3\cdot 0^2-3)(x-0)+f(0) \\ y &= -3x+2 \text{ er\,ligningen\,for\,vendetangenten\,til\,}f(x) \end{align*}$

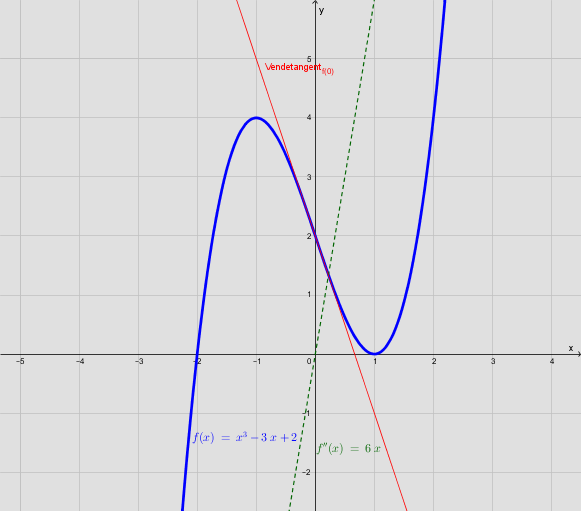
Bemærk at vendetangenten her egentlig ikke tangerer grafen, men skærer denne.

Vedhæftet fil:__0.png

Brugbart svar (0)

Svar #6
19. januar 2020 af ringstedLC

Eks. uden vendetangent:

$\begin{align*} f(x) &= x^2+1 \\ f'(x) &= 2x \\ y &= 2x_0(x-x_0)+f(x_0) \\\\ {\color{Red} f''(x)} &=2=0\Rightarrow f(x)\text{ har\,ingen\,vendetangent(er)} \end{align*}$

Vedhæftet fil:__1.png

Brugbart svar (0)

Svar #7
19. januar 2020 af ringstedLC

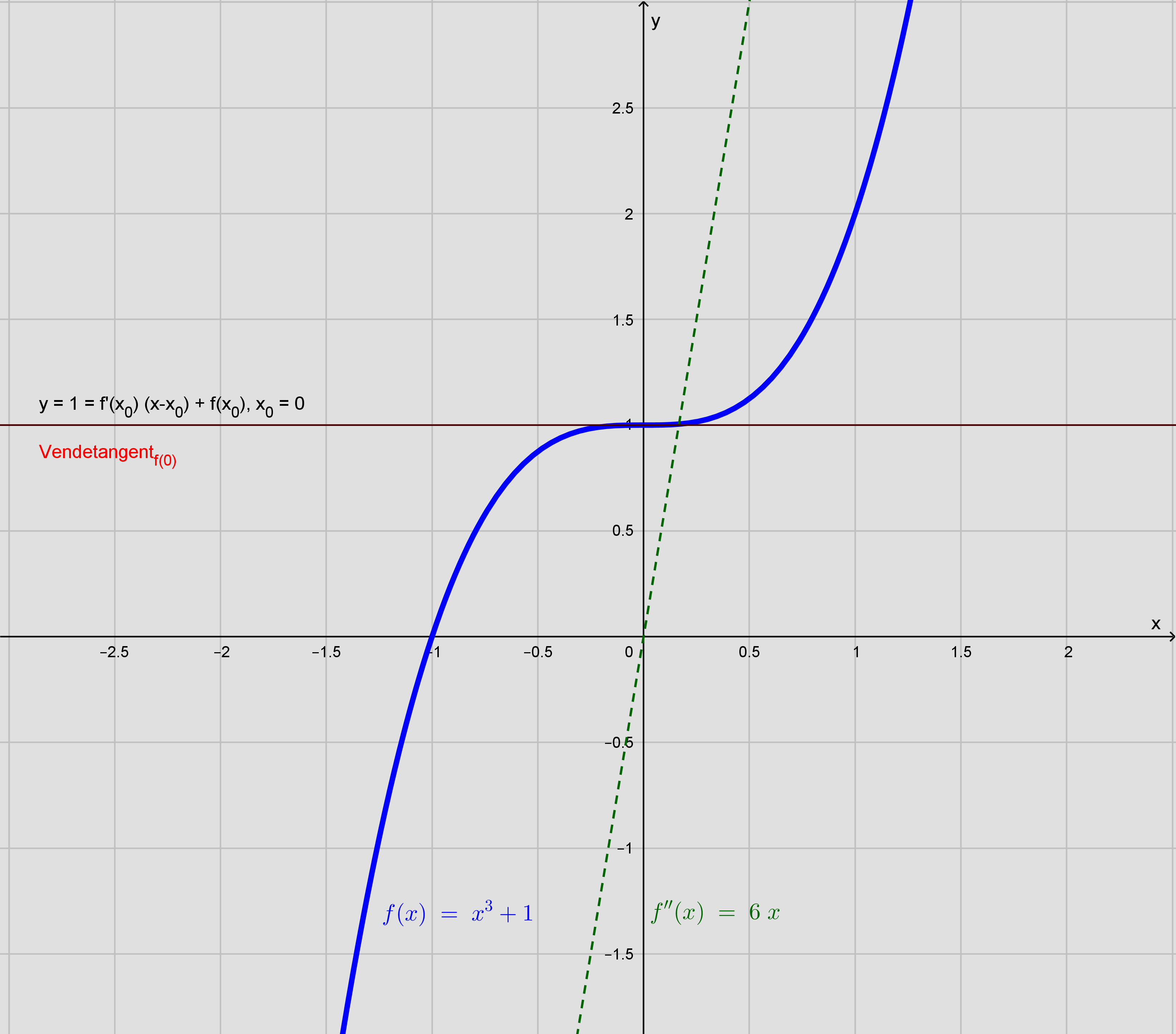
Eks. hvor vendetangent og tangenten i et punkt, hvor f '(x) = 0 er sammenfaldende:

$\begin{align*} f(x) &= x^3+1\\ f'(x) &= 3x^2=0\Rightarrow x=0 \\ y &= f'(x_0)(x-x_0)+f(x_0) \\ y &= 3{x_0}^2(x-x_0)+f(x_0) \\ y &= 1\text{ er\,ligningen\,for\,tangenten\,i\,}f'(x_0)=0 \\ {\color{Red} f''(x)} &= 6x=0\Rightarrow x=0 \\ y &= 3{x_0}^2(x-x_0)+f(x_0) \\ y &= 1\text{ er\,ligningen\,for\,vendetangenten\,til }f(x) \end{align*}$

Vedhæftet fil:__2.png

Skriv et svar til: Vendetangentens ligning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.