Opstil en differentialligning ud fra oplysninger

Her:

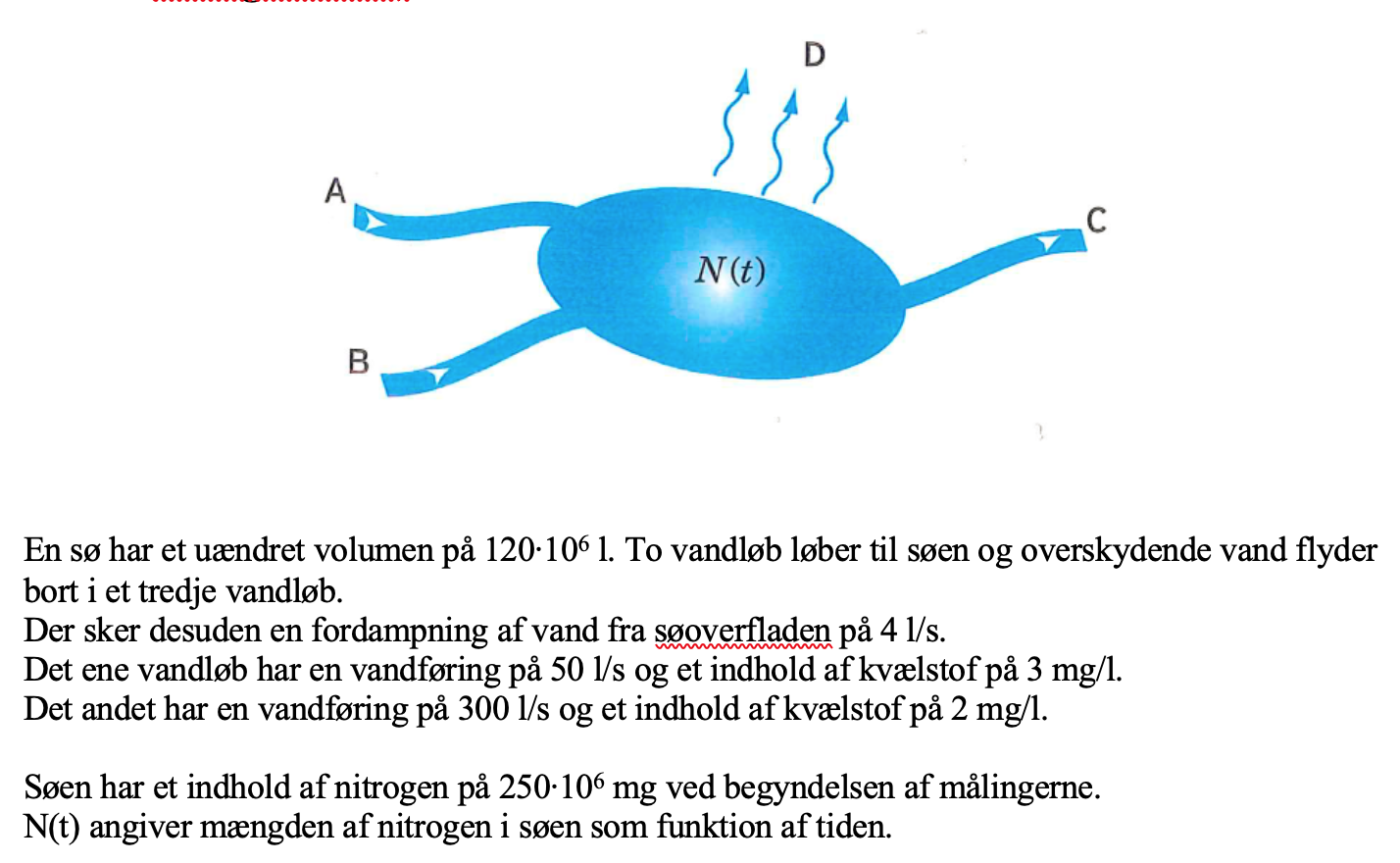
Du skal se på tilførslen af kvælstof pr. sek. og afgøre væksttypen.

Jeg har sagt, at der i søen tilføres 150 mg pr. sek fra vandløb 1 og 600 mg pr. sek fra vandløb to. Så jeg ved ikke, om det så er proportional vækst? Er lidt i tvivl, fordi samtidig er der også vand, som fordamper og ryger ud i et tredje vandløb, og jeg forstår ikke, hvordan det skal med ind i ligningen.

#3: Ja, altså 150 + 600 = 750 mg pr. sek. Det betyder, at N(t) er lineær (b = 250 · 10⁶).

Vedr. din tvivl:

Antag at kvælstoffet bliver i søen fordi det ikke oplyses, om der forsvinder noget.

Som jeg læser det, tilføres der 350L, hvoraf 4L fordamper, og 346L løber ud. Det, der løber ud, må have samme koncentration, som vandet i søen.
Hvis vi antager, at det tilførte vand ikke når at blande sig med det, der løber væk, er koncentrationen (mg/L)
C(t) = N(t)/(120·10⁶). Der forsvinder således ..... mg kvælstof ud i det tredje vandløb
Nettotilførslen (mg pr. sek.) er da N'(t) = 750 - .....

Jeg er med på det første stykke, og at koncentrationen er N(t)/(120*10^6), men forstår ikke helt, hvordan ved, hvor meget kvælstof der ryger ud af det tredje vandløb? 

Der forsvinder 346L med en koncentration på C(t) mg/L, altså 346·C(t) mg.

Så nettotilførsel er altså N'(t) = 750 - 346*c(t)?

I opgaven skal jeg også bestemme indholdet i søen efter 5 måneder, men så forstår jeg ikke hvordan man gør..

#0. Du har: N'(t) = N_A(t) + N_B(t) - N_C(t) 

N_A(t) = V_A·C_A = (50 L/s)·(3 mg/L) = 150 mg/s

N_B(t) = V_B·C_B = (300 L/s)·(2 mg/L) = 600 mg/s

N_C(t) = V_C·C_C = (V_A+V_B-V_D)·(N(t)/V_sø) = (50+300-4)·N(t)/(120·10⁶ L) = (2,833·10^-6 s^-1)·N(t)

N'(t) = (150 mg/s + 600 mg/s) - (2,833·10^-6 s^-1)·N(t) = 750 mg/s - (2,833·10^-6 s^-1)·N(t), N(0) = 250·10⁶ mg.

V står for volumen pr. sek. af væske, C for koncentration af kvælstof.

Tusind tusind tak for hjælpen!! Kan det dog virkelig passe, at indholdet af kvælstof i søen så er nogenlunde konstant, selvom der går længere tid? Jeg har fundet N(t) nu nemlig, og efter 5 måneder er helt samme koncentration som i starten af målingerne.

# 10
N(t) er søens indhold af kvælstof til tiden t i sek efter at indholdet, til tiden 0, var 250 mio mg.
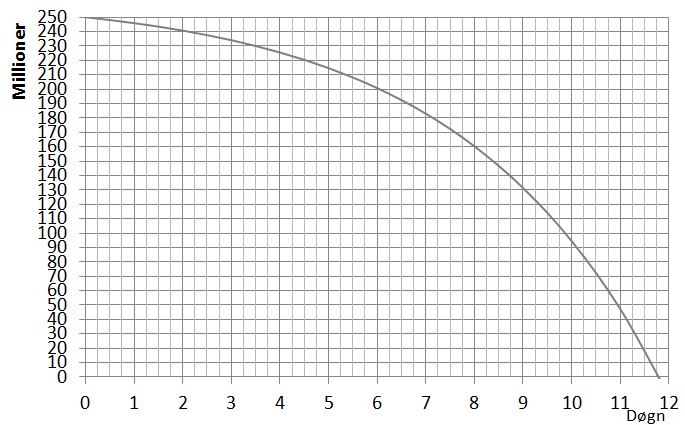
Idet  11 døgn = 950400 sek og 12 døgn = 1036800 sek
finder vi, at søen må være kvælstoffri imellem 11 og 12 døgn efter, der blev målt første gang.
  

#10 Hvad får du N(t) til? Jeg får N(t) = 2.60116·10⁸-1.01156·10^7·0.999997^t .
5 mdr. er ca. 12960000 sek. og på det tidspunkt er kvælstofindholdet iflg. modellen 259.6·10⁶ mg, altså 9.6·10⁶ mg = 9.6 kg større end ved begyndelsen.

#11 Hvordan får du søen til at blive kvælstoffri? Der tilføres vel mindst lige så meget, som der forsvinder? 
Jeg får en øvre grænse på 2.6·10⁸ mg.

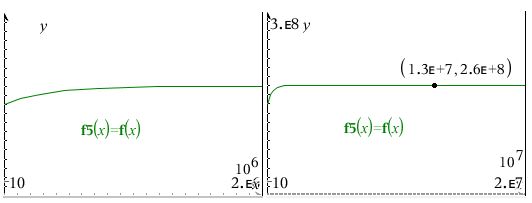
f(x) ~ N(t)

#10. Antag at man har differentialligningen: N'(t) = a - b·N(t), N(0) = c. Den viser, at N(t) starter ved c og nærmer sig a som en eksponentiel udvikling.

.

Med begyndelsesbetingelserne får jeg:

         N(t) = 10⁶· ( 264,737 - 14,737·exp(- 2,833·10^{- 6} ·t) )
som forskrift for kurven # 14

# 11, 14, 16
Ja, beklager, men har overset, at der er et minus i argumentet for exp.
Grænseværdien  N(t) → 264,737·10⁶ for t → ∞ er da rigtignok.
Ja, - et lille minus med den store virkning.

Ad #13 

#10. Antag at man har differentialligningen: N'(t) = a - b·N(t), N(0) = c. Den viser, at N(t) starter ved c og nærmer sig a som en eksponentiel udvikling.

, (Jf. STXA-formelsamling (177) side 29), 
så  og øvre grænse er .

#18.

Øvre grænse = a/b er rigtigt, men det er et andet c, jeg taler om.

ad # 16, # 17
Med en præcis heltallig nedskrivning af forskriften

er grænseværdien, for t →  ,       som også stemmer med # 12.