Matematik

Stykkevist defineret funktion. Forskrift ud fra graf

22. juli 2020 af Haruharu - Niveau: B-niveau

Hej.

jeg stå med to meget ens opgaver som jeg ikke kan se mig ud af.

Opgaven lyder således for begge opgaver:

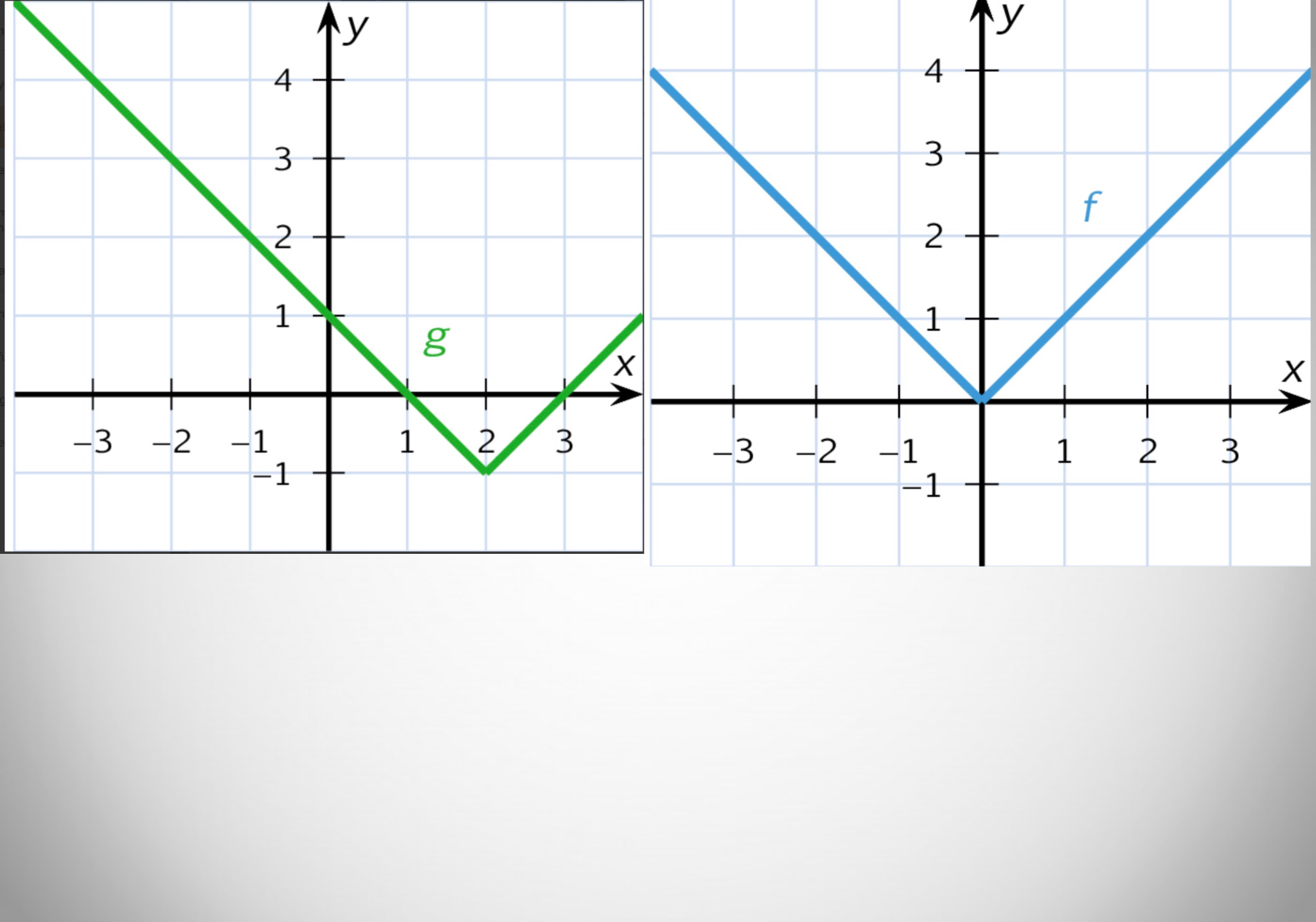
Bestem regneforskrifterne for funktionerne f og g, hvis grafer ses af figurerne (her er graferne vedhæftet)

Vedhæftet fil: 1D2D59D4-6AC0-4C62-B388-CE5C8F5E2D9F.jpeg

Brugbart svar (0)

Svar #1
22. juli 2020 af mathon

Brugbart svar (0)

Svar #2
22. juli 2020 af Forår2020 (Slettet)

forslag til g(x)

g(x) = -x +1 for x < 2 og x-3 for x ≥ 2

Brugbart svar (0)

Svar #3
22. juli 2020 af mathon

$\small \begin{array}{lllll} \textup{funktion:}\\& g(x)=\left\{\begin{array}{lll}-x+1&\textup{for }x\leq 2\\\, \, \, \, x-3&\textup{for }x\geq 2 \end{array}\right.\\\\\\& f(x)=\left\{\begin{array}{lll}-x&\textup{for }x\leq 0\\\, \, \, \, x&\textup{for }x\geq 0 \end{array}\right. \end{array}$

Brugbart svar (0)

Svar #4
22. juli 2020 af Soeffi

#0.

f(x) = |x| og g(x) = |x - 2| - 1.

Benyt evt at: g(x) = f(x - 2) - 1

Svar #5
22. juli 2020 af Haruharu

Tak for svarene, men jeg ønsker en forklaring på hvordan man kan aflæse det. Jeg har facit, jeg ønsker at forstå hvordan jeg kommer hen til det

Brugbart svar (0)

Svar #6
22. juli 2020 af Anders521

# 5 Du er vel klar over, at i begge figurer er der tale om stykkevise linære funktioner, eftersom hver dele af grafen består af rette linjer. Hvilke overvejelser har du gjort dig i forsøg på at løse opgaven?

Brugbart svar (0)

Svar #7
22. juli 2020 af Soeffi

#5...Jeg har facit...

Hvad er facit?

Brugbart svar (0)

Svar #8
22. juli 2020 af mathon

$\small \begin{array}{c|c|c|c|c|c|c} x_1&y_1&x_2&y_2&a=\frac{y_2-y_1}{x_2-x_1}&b=y_1-a\cdot x_1&y=ax+b\\\hline &&&&&& \end{array}$

Brugbart svar (0)

Svar #9
22. juli 2020 af StoreNord

Den grønne grafs funktionsværdi, g(x) blir i starten een mindre, når x vokser med een.
Så er hældningen -1/1 = -1.
Hældningen skriver man som koefficient til x i funktionen.
Den krydser y-aksen i y = +1, som kaldes begyndelsesværdien. Den skriver men som andet led i funktionen.
Så mellem x=-4 og x=2 er funktionen: g(x)=-1x+1
men man behøver ikke at skrive det første 1-tal.

Hvordan funktionerne ser ud udenfor billederne kan vi sådan set ikke vide noget om.

Brugbart svar (0)

Svar #10
22. juli 2020 af mathon

som opfølgning på
#9 Hvordan funktionerne ser ud udenfor billederne kan vi sådan set ikke vide noget om.

$\small \small \begin{array}{lllll} \textup{funktion:}\\& g(x)=\left\{\begin{array}{lll}-x+1&\textup{for }-4\leq x\leq 2\\\, \, \, \, x-3&\textup{for }2\leq x \leq4 \end{array}\right.\\\\\\& f(x)=\left\{\begin{array}{lll}-x&\textup{for }-4\leq x\leq 0\\\, \, \, \, x&\textup{for }0\leq x\leq 4 \end{array}\right. \end{array}$

Brugbart svar (0)

Svar #11
23. juli 2020 af mathon

$\small \begin{array}{c|c|c|c|c|c|c|c} \textup{funktion}&x_1&y_1&x_2&y_2&a=\frac{y_2-y_1}{x_2-x_1}&b=y_1-a\cdot x_1&y=ax+b\\\hline g(x)&0&1&2&-1&a=\frac{-1-1}{2-0}=-1&b=1-(-1)\cdot 0=1&y=-x+1\\ &&&&&&&\\ g(x)&2&-1&4&1&a=\frac{1-(-1)}{4-2}=1&b=-1-1\cdot 2=-3&y=x-3 \end{array}$

Brugbart svar (0)

Svar #12
23. juli 2020 af mathon

$\small \small \begin{array}{c|c|c|c|c|c|c|c} \textup{funktion}&x_1&y_1&x_2&y_2&a=\frac{y_2-y_1}{x_2-x_1}&b=y_1-a\cdot x_1&y=ax+b\\\hline f(x)&-3&3&0&0&a=\frac{0-3}{0-(-3)}=-1&b=3-(-1)\cdot (-3)=0&y=-x\\ &&&&&&&\\ f(x)&3&3&0&0&a=\frac{0-3}{0-3}=1&b=3-1\cdot 3=0&y=x \end{array}$

Svar #13
23. juli 2020 af Haruharu

Tak, jeg tror jeg forstår det nogenlunden nu. Tak for hjælpen til alle

Skriv et svar til: Stykkevist defineret funktion. Forskrift ud fra graf

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.