Matematik
Areal af Gavle
Hej Alle
jeg har den opgave som har taget meget af min tid og kunne ikke beregne den indtil videre
håber at nogle kan hjælp mig med.
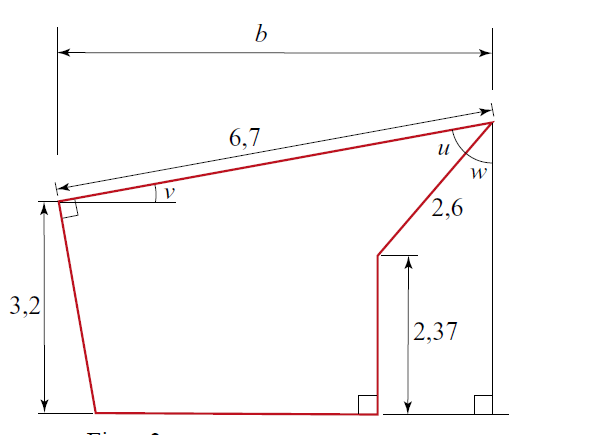
" på selv figuren bygningens sidegavl vist med mål. Alle længder er i meter. Vinkel u = 40 og vinkel w er 40 og vinkel v er 10
Vi skal bestemme sidegavlens Areal?
Figuren vedhæftes
Tak på forhånden.
Svar #2
22. september 2020 af peter lind
Hvad er gavlen ? For mig ser arealet afgrænset med det røde omrids ikke ud som en gavl. Hvad har du selv fundet af evt. manglende værdier ? Kom med hele opgaven gerne som billedfil eller pdf fil.
Svar #5
22. september 2020 af Soeffi
#4.
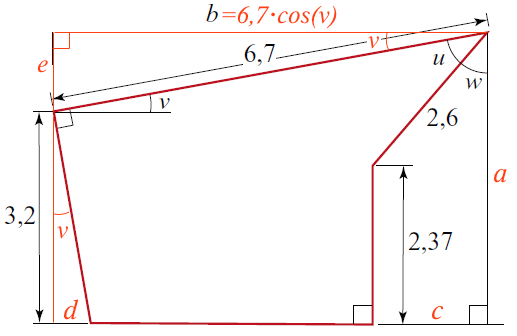
a = 2,6·cos(w), b = 6,7·cos(v), c = 2,6·sin(w), d = 3,2·tan(v) og e = 6,7·sin(v).
Svar #6
22. september 2020 af DeepOcean
er kendte i den trekant som du beregne d
Hvorfor der? Hvordan kan du konkluderer at den v vinkel i trekant som beregnes d er samme som er givet i figuren hvor v vinkel er 10?
Svar #7
23. september 2020 af Soeffi
#6.
Man kan se sådan på det, at der er 90° mellem taget og venstre side af gavlen. Når disse sider begge drejes vinklen v med uret, så kommer man over i en vandret og en lodret linje. Derfor er der v grader mellem gavlens venstre side pg lodret.
Svar #8
23. september 2020 af Soeffi
#3...
Areal af ydre rektangel: a·b = 6,7·cos(10°)·(2,37+2,6·cos(40°)) = 6,5982·4,3617 = 28,780.
Areal af trekant med siden d: 0,5·3,2·d = 0,5·3,22·tan(v) = 0,5·3,22·tan(10°) = 0,90279.
Areal af trekant med siden b: 0,5·b·e = 0,5·6,72·cos(10°)·sin(10°) = 0,5·6,72·0,98481·0,17365 = 3,8383.
Areal af rektangel med siden c: 2,37·c = 2,37·2,6·sin(40°) = 3,9609.
Areal af trekant med siden 2,6: 0,5·2,62·cos(40°) = 0,5·2,62·0,76604 = 1,0035.
Areal af gavl: 28,780 - (0,90279 + 3,8383 + 3,9609 + 1,0035) = 19,075
Svar #10
16. februar 2021 af Ukendterjeg
#8#3...
Areal af ydre rektangel: a·b = 6,7·cos(10°)·(2,37+2,6·cos(40°)) = 6,5982·4,3617 = 28,780.
Areal af trekant med siden d: 0,5·3,2·d = 0,5·3,22·tan(v) = 0,5·3,22·tan(10°) = 0,90279.
Areal af trekant med siden b: 0,5·b·e = 0,5·6,72·cos(10°)·sin(10°) = 0,5·6,72·0,98481·0,17365 = 3,8383.
Areal af rektangel med siden c: 2,37·c = 2,37·2,6·sin(40°) = 3,9609.
Areal af trekant med siden 2,6: 0,5·2,62·cos(40°) = 0,5·2,62·0,76604 = 1,0035.
Areal af gavl: 28,780 - (0,90279 + 3,8383 + 3,9609 + 1,0035) = 19,075
“Areal af trekant med siden 2,6" giver ikke 1,0035, men 1,664325, ellers fornuftigt forklaret.
Skriv et svar til: Areal af Gavle
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.