Matematik
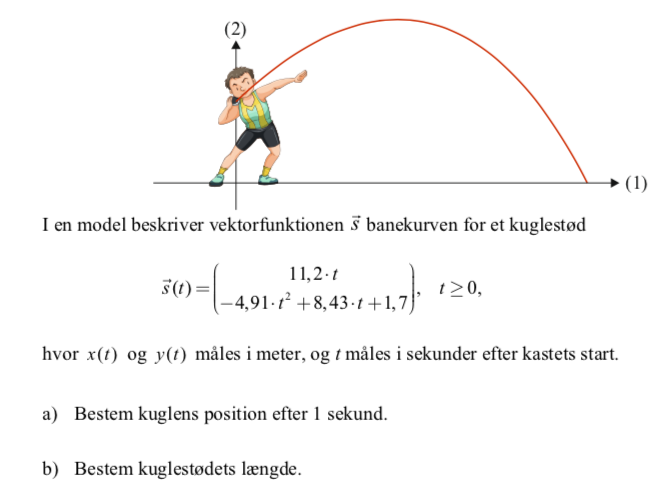
Vektorfunktion og kuglen
Jeg har følgende opgave som jeg ikke ved hvad jeg skal gøre???
Svar #2
24. oktober 2020 af peter lind
a) Sæt t = 1 i vektorligningen og beregn
b) Løs ligningen y(t) = 0. Der vil være to løsninger. Vælg den positive t0. Derefter finder du kuglestødets længde ved at beregne x(t0)
Svar #3
24. oktober 2020 af Trojanskhest
Hej Peter,
a)
Betyder det bare at kuglens position er
s(1)=vector(11.2,5.22)
??
Synes bare det er mærkeligt at man vektoreren kan forklarer om positionen.
Svar #4
24. oktober 2020 af peter lind
Jeg har ikke regnet efter; men x koordinaten er OK. Vektorfunktionen angiver jo hvor kuglen er til tiden t
Svar #6
25. oktober 2020 af ringstedLC
#3Synes bare det er mærkeligt at man vektoreren kan forklarer om positionen.
Vektoren med parameteren t beskriver et punkt på kurven som svarer til funktionen:
men vektorfunktionen er jo mere overskuelig:
Skriv et svar til: Vektorfunktion og kuglen
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.