Matematik

Skal der bruges substuition integrale?

28. december 2020 af Amalie1234324 - Niveau: A-niveau

Hejsa :),

Jeg sidder med en opgave hvor jeg er lidt i tvivl om der kan bruges substiution. Det er på følgende x^5*cos(6x).

Jeg tænkte at substution kan bruges, da hvis x^5 diffirenteres kan x^et i ved 6x gå ud, hvilket er målet. Så jeg havde tænkt mig at diffirentere x^5 og får dx= du/5x.

NB: Jeg er godt klar over der skal bruges produktreglen og kædelreglen undervejs.

Vedhæftet fil: Billede1.jpg

Brugbart svar (0)

Svar #1
28. december 2020 af Anders521

#0 Dit resultat er korrekt. Substitution bruges i forbindelse med integration, ikke differentation. Bemærk, at overskriften og den vedhæftede opgave ikke stemmer overens.

Brugbart svar (0)

Svar #2
28. december 2020 af peter lind

Brug hellere gentagne partielintegration. Differentier xⁱ integrer cos(6x) eller sin(6x). Du får faldende potense fra 5.potens og ned til 0 og skiftevis cosinus og sinus

Brugbart svar (0)

Svar #3
28. december 2020 af ringstedLC

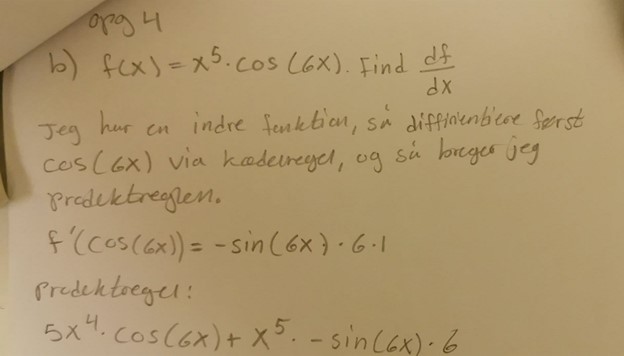
Du skriver integrale i overskriften, men opgaven siger differentiale, og det gøres korrekt, men kan dog reduceres.

Svar #4
28. december 2020 af Amalie1234324

Ja det kan jeg godt se. Det er hvad der sker når man siddet oppe hele dagen og forberedt sig haha.

Brugbart svar (0)

Svar #5
28. december 2020 af ringstedLC

#0
x^5 og får dx= du/5x.

$\begin{align*} \frac{\mathrm{d} u}{\mathrm{d} x}&= 5x^4 \\ \mathrm{d} x &=\frac{\mathrm{d} u}{5x^4} \end{align*}$

#4: "... siddet oppe hele dagen..." , skulle måske have været hele natten. Hold en pause, gå en tur og fortsæt så.

Svar #6
28. december 2020 af Amalie1234324

Vil det være rigtigt nok at vælge u til x i denne: " løs integralet integral af x*cos(2x), for det bliver ikke mere kompliceret at integrere cos(2x), og at diffirentere cos(2x) gør det heller ikke nemmer?

Snakke om hvilket der skal være v og hvilket der skal være dv

Brugbart svar (0)

Svar #7
28. december 2020 af peter lind

Hvad vil du ? Integrere eller differentiere ?

Det er rigtig at det bliver hverken sværere eller lettere at vælge 2x eller 6x eller for den sags skyld ax a≠0

Svar #8
29. december 2020 af Amalie1234324

Jeg skal vel begge dele ved partiel integration integral u*v-integral af v*du.

SÅ jeg skal vælge en der skal diffireniteres og en der skal integreres. Vil det være ligemeget hvilken en jeg tager.

Brugbart svar (0)

Svar #9
29. december 2020 af AskTheAfghan

#0 Man skriver (cos(6x))', ikke f '(cos(6x)).

#8 Hvis du ønsker at integrere noget, venligst upload hele opgave, så det ikke skaber nogle misforståelser.

Svar #10
29. december 2020 af Amalie1234324

Her er den

Vedhæftet fil:den her.PNG

Brugbart svar (0)

Svar #11
29. december 2020 af mathon

$\small \begin{array}{lllll} \textup{funktion}:&f(x)=\cos(2x)\cdot x\\\\ \textup{integralet:}&\int \cos(2x)\cdot x\,\mathrm{d}x=\frac{1}{2}\sin(2x)\cdot x-\frac{1}{2}\int \sin(2x)\cdot 1\,\mathrm{d}x=\frac{1}{2}x\sin(2x)+\frac{1}{4}\cos(2x)+k \end{array}$

Svar #12
29. december 2020 af Amalie1234324

Jeg forstår at du har valgt u til x og dv til cos(2X). Så i det du har lave er v=sin(2x). Men så forstår jeg ikke hvordan du indsætter i formlen u*v-integral af v*du..

Hvorfor har dit v(som er sin(2x) 1/2 stående ved siden af i starten af formlen. u indsættes fint som er x?

Brugbart svar (0)

Svar #13
29. december 2020 af mathon

$\small \small \begin{array}{lllll} \textup{funktion}:&f(x)=\cos(2x)\cdot x\\\\ \textup{integralet:}&\int \cos(2x)\cdot x\,\mathrm{d}x=\frac{1}{2}\sin(2x)\cdot x- \int \frac{1}{2}\sin(2x)\cdot 1\,\mathrm{d}x=\frac{1}{2}x\sin(2x)-\frac{1}{2}\cdot \frac{1}{2}\cdot \left ( -\cos(2x) \right )+k\\\\& \int \cos(2x)\cdot x\,\mathrm{d}x=\frac{1}{2}x\sin(2x)+\frac{1}{4}\cos(2x)+k \end{array}$

Svar #14
29. december 2020 af Amalie1234324

Hvis du har integreret cos(2x), så giver det vel sin(2x) kun, uden en halv?

Brugbart svar (0)

Svar #15
29. december 2020 af Anders521

#14 Det kan du vel selv undersøge. Hvad sker hvis du differentierer sin(2x) "uden en halv" på? Får du cos(2x)?

Svar #16
30. december 2020 af Amalie1234324

Sin(2x) diffireinteret giver ikke cos(2x). Hvor kommer det halve fra?

Brugbart svar (1)

Svar #17
30. december 2020 af ringstedLC

$\begin{align*} \int \!f(a\cdot x+b)\,\mathrm{d}x &= \tfrac{1}{a}\cdot F(a\cdot x+b) \end{align*}$

Brugbart svar (0)

Svar #18
01. januar 2021 af ringstedLC

#12: Noget kunne tyde på, at du gerne vil bruge:

$\begin{align*} \int\! u\cdot \mathrm{d} v &= u\cdot v- \!\int\! v\cdot \mathrm{d} u \end{align*}$

Her skal man bemærke, at funktionerne ikke kan indsættes direkte:

$\begin{align*} \mathrm{d} u &= u'(x)\,\mathrm{d} x \\ \mathrm{d} v &= v'(x)\,\mathrm{d} x \\ \int\! u\cdot \mathrm{d} v &= u\cdot v-\!\int\! v\cdot \mathrm{d} u \\ \int\! u\cdot v'(x)\,\mathrm{d} x &= u\cdot v- \!\int\! v\cdot u'(x)\,\mathrm{d} x \\ \end{align*}$

$\begin{align*} \int\! x\cdot \cos(2x) &\Rightarrow \left\{\begin{matrix} \qquad\;x\!&\!= u\;\, \!&\! \Rightarrow \mathrm{d} u \!&\!= \mathrm{d} x \qquad\quad \;\;& \\ \cos(2x) \!&\!= \mathrm{d} v \!&\! \Rightarrow \;\;v \!&\!= \!\int\! \cos(2x) \,\mathrm{d} x \!&\!= \tfrac{1}{2}\cdot \sin(2x)^{*\,\text{se note!}}& \end{matrix}\right. \\ &= x\cdot \tfrac{1}{2}\cdot \sin(2x)-\!\int\! \tfrac{1}{2}\cdot \sin(2x)\,\mathrm{d} x \\ &= \tfrac{1}{2} x\cdot \sin(2x)-\tfrac{1}{2}\cdot \!\int\! \sin(2x)\,\mathrm{d} x \\ &= \tfrac{1}{2} x\cdot \sin(2x)-\tfrac{1}{2}\cdot \bigl(-\tfrac{1}{2}\cdot \cos(2x)\bigr) \\ &= \tfrac{1}{2} x\cdot \sin(2x)+\tfrac{1}{4}\cdot \cos(2x)-k \end{align*}$

*Mellemregninger med int.-konstanter er udeladt for overskulighed.

Brugbart svar (0)

Svar #19
01. januar 2021 af ringstedLC

I #11 (og #13) bruges:

$\begin{align*} \int\! f(x)\cdot g(x)\,\mathrm{d} x &= f(x)\cdot G(x)- \!\int\! f'(x)\cdot G(x)\,\mathrm{d} x \;,\;G(x)= \!\int\! g(x)\,\mathrm{d} x \end{align*}$

hvor funktionerne kan indsættes direkte:

$\begin{align*} \int\! x\cdot \cos(2x)\,\mathrm{d} x &= x\cdot \!\int\! \cos(2x)\,\mathrm{d} x- \!\int \!\Bigl(\bigl(x\bigr)'\cdot \!\!\int \!\cos(2x)\,\mathrm{d}x\!\Bigr) \,\mathrm{d} x \\ &= x\cdot \Bigl(\tfrac{1}{2}\cdot \sin(2x)+k_1\Bigr)-\!\int \!1\cdot \Bigl(\tfrac{1}{2}\cdot \sin(2x)+k_2\Bigr)\,\mathrm{d} x \\ &= \tfrac{1}{2}x\cdot \sin(2x)+k_1x-\Bigl(-\tfrac{1}{4}\cdot \cos(2x)+k_2x+k_3\Bigr) \\ &= \tfrac{1}{2}x\cdot \sin(2x)+\tfrac{1}{4}\cdot \cos(2x)-k_3+k_1x-k_2x \\ &= \tfrac{1}{2}x\cdot \sin(2x)+\tfrac{1}{4}\cdot \cos(2x)-k_3\;,\;k_1=k_2 \end{align*}$

Her vist med mellemregninger af int.-konstanter.

Brugbart svar (0)

Svar #20
01. januar 2021 af ringstedLC

#18 suppl.: Ved at arbejde videre med "din" formel, fås:

$\begin{align*} \int\! u\cdot v &= u\cdot v- \!\int\! v\cdot \mathrm{d} u \\ u\cdot v &= \!\int\! u\cdot \mathrm{d} v+\!\int\! v\cdot \mathrm{d} u \\ &= \!\int\! u\cdot \mathrm{d} v+v\cdot \mathrm{d} u \\ \bigl(u(x)\cdot v(x)\bigr)' &= u(x)\cdot v'(x)+v(x)\cdot u'(x) \;,\; \left\{\begin{matrix}u=u(x) \Rightarrow \mathrm{d} u=u'(x) \\v=v(x) \Rightarrow \mathrm{d} v=v'(x)\end{matrix}\right. \end{align*}$

der kendes som produktreglen, anvendelig til at differentiere et produkt af funktioner.

Skriv et svar til: Skal der bruges substuition integrale?

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.