Matematik

Om en ikke retvinklet trekant oplyses - Bestem a, B og C

22. februar 2021 af JulieH004 - Niveau: B-niveau

Hvordan løser jeg opgaven?

Hvilken formel skal jeg bruge?

Vedhæftet fil: 123.PNG

Brugbart svar (0)

Svar #1
22. februar 2021 af janhaa

a: use cosine law

B and C: use sine law

a = 5,14

Brugbart svar (0)

Svar #2
22. februar 2021 af ringstedLC

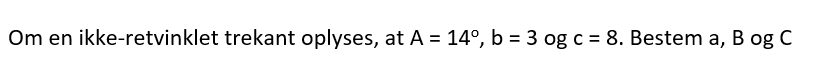
Med én vinkel og dens vinkelben bruges cosinusrelationen, først til a og siden til fx B. Sidste vinkel kan findes med vinkelsummen (180º).

Brugbart svar (0)

Svar #3
23. februar 2021 af mathon

Hvis du bruger vinkelsummen på 180° til at beregne den sidste vinkel, opdager du aldrig en eventuel vinkelfejl.

Bruges vinkelsummen på 180° som kontrol, afdækkes en evt. vinkelfejl.

Brugbart svar (0)

Svar #4
23. februar 2021 af mathon

$\small \begin{array}{lllll} a=\sqrt{b^2+c^2-2\cdot b\cdot c\cdot \cos(A)}\\\\ B=\cos^{-1}\left ( \frac{a^2+c^2-b^2}{2a\cdot c} \right )\\\\ C=\cos^{-1}\left ( \frac{a^2+b^2-c^2}{2a\cdot b} \right ) \end{array}$

Brugbart svar (0)

Svar #5
24. februar 2021 af mathon

efter oprettelse af endnu en tråd med samme opgave:
https://www.studieportalen.dk/forums/thread.aspx?id=2001029

$\small \small \begin{array}{llr} a=\sqrt{b^2+c^2-2\cdot b\cdot c\cdot \cos(A)}=\sqrt{3^2+8^2-2\cdot 3\cdot 8\cdot \cos(14\degree)}&=&5.14\\\\ B=\cos^{-1}\left ( \frac{a^2+c^2-b^2}{2a\cdot c} \right )=\cos^{-1}\left ( \frac{5.14^2+8^2-3^2}{2\cdot 5.14 \cdot 8} \right )&=&8.10\degree\\\\ C=\cos^{-1}\left ( \frac{a^2+b^2-c^2}{2a\cdot b} \right )=\cos^{-1}\left ( \frac{5.14^2+3^2-8^2}{2\cdot 5.14\cdot 3} \right )&=&157.9\degree \end{array}$

Skriv et svar til: Om en ikke retvinklet trekant oplyses - Bestem a, B og C

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.