Matematik

Vektorer (koefficient)

04. marts 2021 af Kathrinethomseen - Niveau: A-niveau

Godaften

Jeg mangler lidt hjælp til vedhæftede opgave:

Vedhæftet fil: Skærmbillede 2021-03-04 kl. 20.50.31.png

Brugbart svar (0)

Svar #1
04. marts 2021 af peter lind

Skriv ligningen ud for henholdsvis første koordinaten og anden koordinaten. Det giver to ligninger med 2 ubekendte som du må løse

Brugbart svar (0)

Svar #2
04. marts 2021 af mathon

$\small \small \begin{array}{llllll} \begin{matrix} 2x&-&y&=&1\\-6x&+&4y&=&2 \end{matrix} \end{array}$

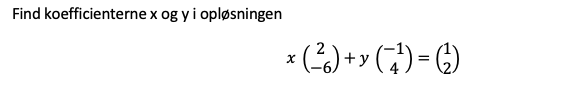
Svar #3
05. marts 2021 af Kathrinethomseen

Jeg forstår ikke, hvad det er jeg skal.

Jeg har vedhæftet, det jeg har lavet, men ved ikke om det er rigtigt?

Vedhæftet fil:Skærmbillede 2021-03-05 kl. 10.05.14.png

Brugbart svar (0)

Svar #4
05. marts 2021 af mathon

Løs de to ligninger med to ubekendte
for at finde koefficienterne.

Svar #5
05. marts 2021 af Kathrinethomseen

Men dette jeg har vedhæftet, er det rigtigt?

Og hvilke to ligninger med to ubekendte mener du?

Brugbart svar (0)

Svar #6
05. marts 2021 af mathon

$\small \begin{array}{llllll}& \begin{matrix} I\textup{:}&2x&-&y&=&1\\II\textup{:}&-6x&+&4y&=&2 \end{matrix} \\\\ \textup{Multiplicer I med 3}&\textup{og regn videre.} \end{array}$

Brugbart svar (0)

Svar #7
05. marts 2021 af mathon

Du kan jo kontrollere
dit resultat ved CAS beregning:

$\small \textup{solve}\left ( 2x-y=1 \textup{ and }-6x+4y=2,\left \{ x,y \right \} \right )$

Svar #8
06. marts 2021 af Kathrinethomseen

Okay, tusind tak!

Så koefficienterne x og y er: x = 1 og y = 2??

Eller er jeg helt væk?

Brugbart svar (0)

Svar #9
06. marts 2021 af ringstedLC

#8: Når du fundet en løsning på en ligning, kan den kontrolleres ved at indsætte den i den oprindelige ligning og se om den er opfyldt, altså om venstre side er lig højre side. Ved ligningssæt skal løsningsparret opfylde begge ligninger.

x og y er variabler, ikke koefficienter.

Brugbart svar (0)

Svar #10
07. marts 2021 af mathon

$\small \small \small \begin{array}{llllll}& \begin{matrix} I\textup{:}&2x&-&y&=&1\\II\textup{:}&-6x&+&4y&=&2 \end{matrix} \\\\ \textup{Multiplicer I med 3:}\\\\\\& \begin{array}{llllll} III\textup{:}&6x &-& 3y&=&3\\II\textup{:}& \! \! \! \! \! -6x&+&4y&=&2 \end{array} \\\\ III \textup{ og }II\textup{ adderes:}\\& y=5\\ \textup{som indsat i }I\\ \textup{giver:}\\& 2x-5=1\\\\& x=3 \end{array}$

Brugbart svar (0)

Svar #11
07. marts 2021 af mathon

kontrol:

$\small \begin{array}{lllll} x\cdot \begin{pmatrix} 2\\-6 \end{pmatrix}+y\cdot \begin{pmatrix} -1\\4 \end{pmatrix}=3\cdot \begin{pmatrix} 2\\-6 \end{pmatrix}+5\cdot \begin{pmatrix} -1\\4 \end{pmatrix}=\begin{pmatrix} 6\\-18 \end{pmatrix}+\begin{pmatrix} -5\\20 \end{pmatrix}=\begin{pmatrix} 1\\2 \end{pmatrix} \end{array}$

Skriv et svar til: Vektorer (koefficient)

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.