Matematik

Hjælp til matematik projekt

24. april 2021 af FillipWiller - Niveau: B-niveau

Hej derude, jeg har desperat brug for hjælp til opgave b som kan ses på billedet. Jeg har i langtid nu prøvet på at løse den men kan ikke finde ud af det, håber i kan hjælpe mig:)

Vedhæftet fil: Skærmbillede 2021-04-24 kl. 14.17.37.png

Brugbart svar (0)

Svar #1
24. april 2021 af mathon

Brugbart svar (0)

Svar #2
24. april 2021 af StoreNord

#0
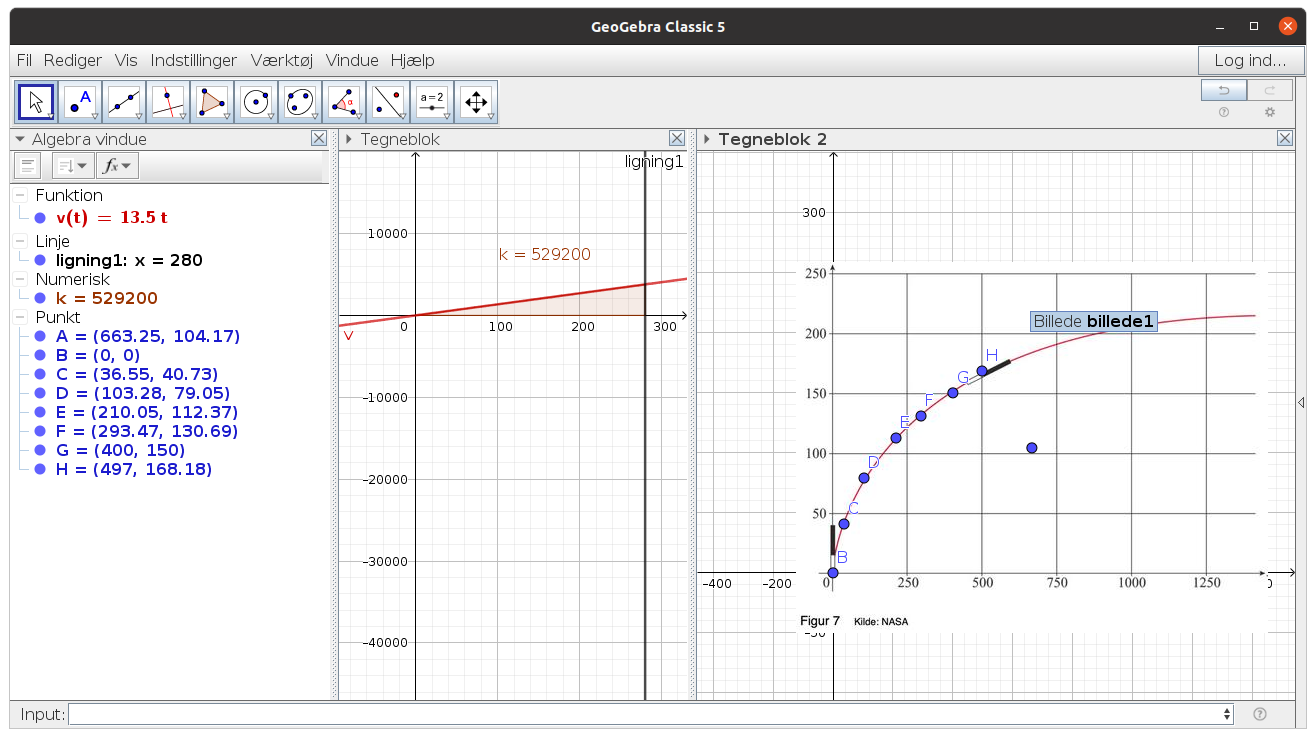
Jeg tror du skal lægge billedet af grafen (som .jpg) ind i geogebra, og så placere nogle støttepunkter på grafen.
Så kan du lave regression for at finde funktionen eller beregninger udfra disse støttepunkter.

Vedhæftet fil:Skærmbillede fra 2021-04-24 17-24-54.png

Brugbart svar (0)

Svar #3
24. april 2021 af mathon

$\small \begin{array}{llllll} \textbf{a)}\\&& s=\int_{0}^{280} v(t)\,\mathrm{d}t=\int_{0}^{280} 13.5\cdot t\,\mathrm{d}t \\\\\\ \textbf{b)}\\&& 170=\int_{0}^{a} 13.5\cdot t\,\mathrm{d}t\\\\&& 170=\left [6.75\cdot t^2 \right ]_{0}^{a}=6.75\cdot a^2\quad a>0\\\\&& a=\sqrt{\frac{170}{6.75}}=5.02\\\\& \textup{Optegn kurven}\\&& v(t)\quad \textup{i intervallet}\quad \left [ 0\, ;5.02 \right ] \end{array}$

Brugbart svar (0)

Svar #4
25. april 2021 af mathon

Korrektion:
$h(t)=6.75\cdot t^2\quad t\in\left [ 0;5.02 \right ]$

Brugbart svar (0)

Svar #5
25. april 2021 af bsj2002

Hej jeg har sammen opgave

Jeg forstå ikke hvad der bliver fundet frem til i udregningen af b) i svar#3

Kan slet ikke få det til at hænge sammen, også selvom jeg laver støttepunkter i GeoGebra

Brugbart svar (0)

Svar #6
25. april 2021 af bsj2002

Hvad betyder tallet [0;5.02]?

Brugbart svar (0)

Svar #7
25. april 2021 af mathon

...ikke et tal men et interval.

Brugbart svar (0)

Svar #8
25. april 2021 af ringstedLC

Raketten følger en ballistisk bane (≈ kasteparabel), der gerne skulle være så stor, at den ikke lander igen. Det vil sige, at dens fart bringer den i kredsløb om Jorden.

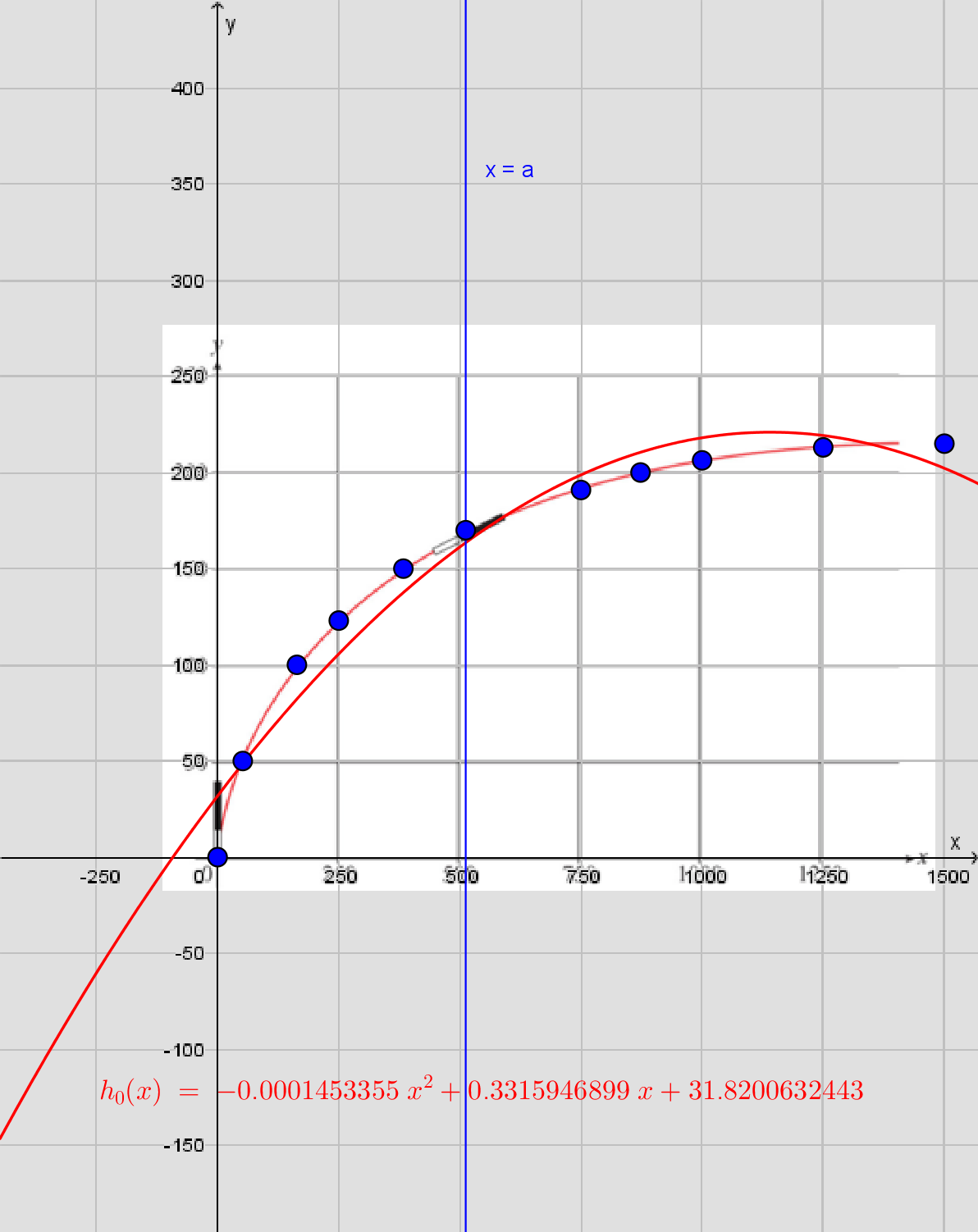
Indlæg tegningen af rakettens bane vha. opgavens vejledning og følg #2's råd om støttepunkter. Brug GG funktionen "FitPoly" (2. grads) på støttepunkterne eller regress. for at bestemme h(x) og differentier den:

$\begin{align*} h(x) &= \,... \\ h'(x) &= \,... \end{align*}$

Da grafens længde fra startpunktet og til raketten er den tilbagelagte afstand på 280 sek., bruges formel (89) for længden af en graf for at bestemme intervallet for h(x):

$\begin{align*} L\cdot 10^3 &= s(280) \quad \bigl(L\,\text{er\,i\,km}, \;s\,\text{er\,i\,m}\bigr) \\ \int_{0}^{a}\!\sqrt{1+h'(x)^2}\,\mathrm{d}x\cdot 10^3 &= \int_{0}^{280}\!v(t)\,\mathrm{d}t \\ a &= \;? \\ \Rightarrow h(x) &=\,...\;,\;0\leq x\leq \;? \end{align*}$

Vedhæftet fil:__1.png

Brugbart svar (0)

Svar #9
25. april 2021 af ringstedLC

Her ses rakettens bane i et nogenlunde forhold til Jorden. Højden er ca. 220 km og farten er ca. 3780 m/s.

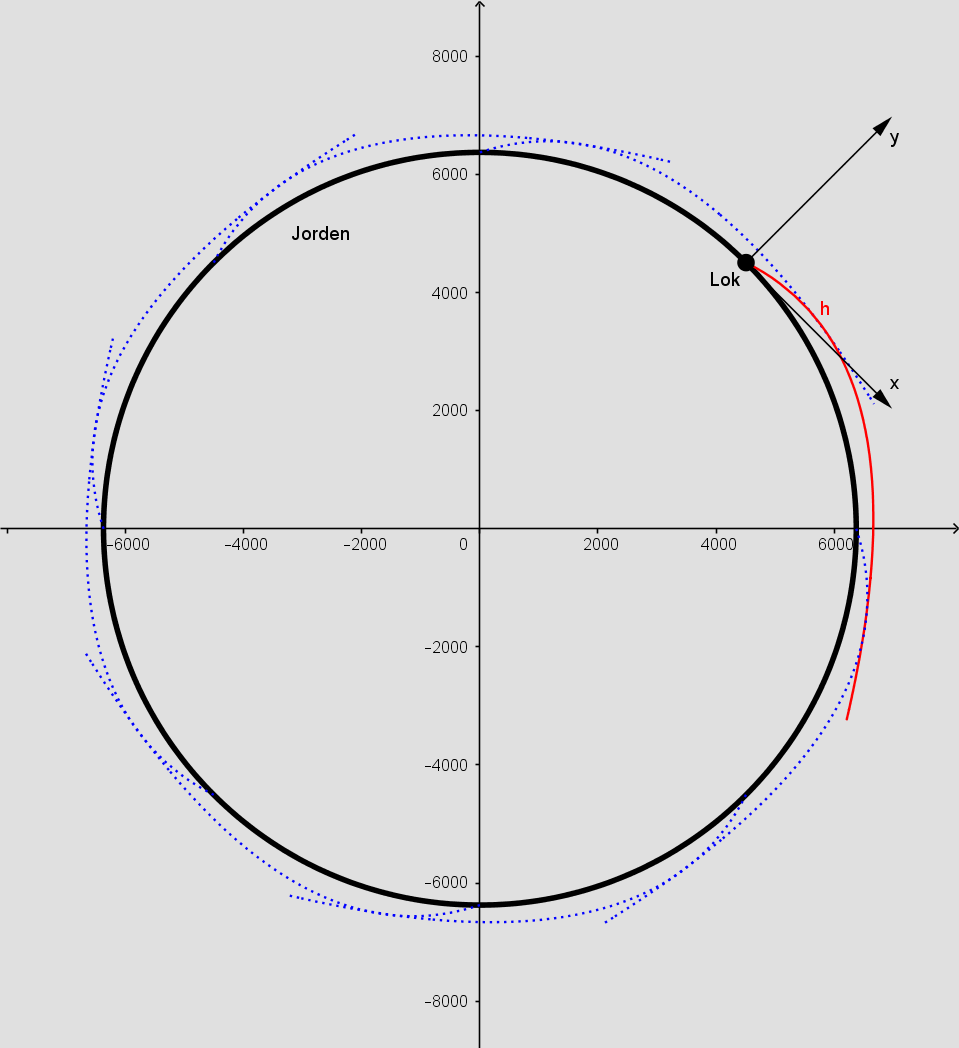
Hvis raketten skal højere op, må farten øges. Den Internationale Rumstation (ISS) kredser i en højde af ca. 386 km med farten ca. 7700 m/s.

Vedhæftet fil:__0.png

Brugbart svar (0)

Svar #10
25. april 2021 af mathon

Sorry - jeg læste det som "højden".

Brugbart svar (0)

Svar #11
06. maj 2021 af asiel2002

jeg forstår ikke helt disse to delopgaver

Vedhæftet fil:Skærmbillede 2021-05-06 kl. 14.53.12.png

Brugbart svar (0)

Svar #12
06. maj 2021 af ringstedLC

c) Raketten følger banen på figur 7 til højden 170 km. Banen forskrift har du bestemt. Da formlen giver længden af grafen for en funktion, raketten starter i x = 0 og integralet af hastighed v(t) er lig strækning, kan ligningen i #8 opstilles og løses for a.

d) De 400 er kilometer på jordoverfladen. h(x) er højden over Jorden.

Skriv et svar til: Hjælp til matematik projekt

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.