Matematik
Vektorer spørgsmål?
Hej,
Jeg skal lave de her spørgsmål i matematik, og ville hører om der var en nemmere måde at gøre dem?
Opgaverne lyder:
- Find ud af om denne firkant ABCD, er en rektengel? Man får 4 koordinater.
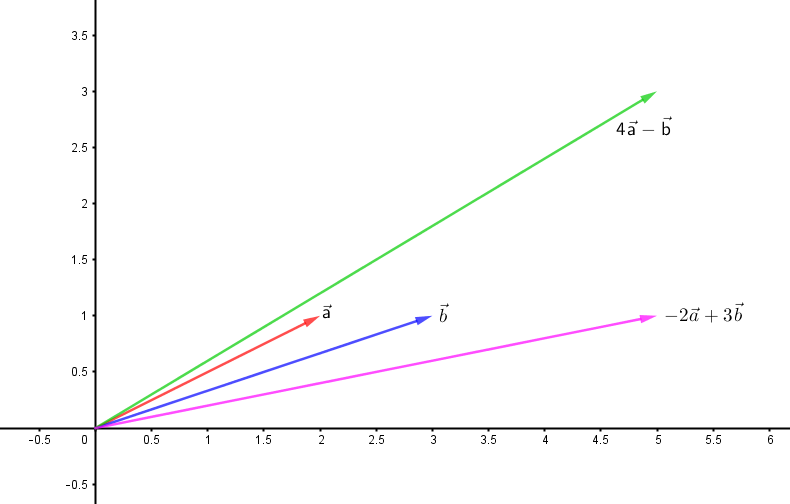
- Du har følgende vektorer (2,1) og (3,1) + find ud af om (4*a-b) samt (-2*a+3*b) er vinkelrette med hinanden?
Er der en hurtig og sikker måde at regne disse?
Jeg ved at den første er vinkelret ved at gøre det grafisk, men er ikke helt sikker på hvordan det skal gøres når man skal regne det?
Tak,
Svar #1
05. maj 2021 af PeterValberg
To vektorer er ortogonale (vinkelrette), hvis deres skalarprodukt er lig med nul,
det er det, du skal undersøge....
#1To vektorer er ortogonale (vinkelrette), hvis deres skalarprodukt er lig med nul,
det er det, du skal undersøge....
Jeg havde på fornemmelsen at jeg skulle bruge skalarproduktet, men kan jeg bruge skalarproduktet alene, eller skal jeg kombinere den med andre formler?
#2#1To vektorer er ortogonale (vinkelrette), hvis deres skalarprodukt er lig med nul,
det er det, du skal undersøge....Jeg havde på fornemmelsen at jeg skulle bruge skalarproduktet, men kan jeg bruge skalarproduktet alene, eller skal jeg kombinere den med andre formler?
på fx den første
Svar #4
05. maj 2021 af PeterValberg
Hvis:
og
så skal du finde ud af om vektoren 4a+b og vektoren -2a+3b er ortogonale,
bestem koordinaterne for hhv. 4a+b og -2a+3 og undersøg om deres skalarprodukt er lig med 0
jeg kan give resten af informationerne:
1. A(-1,2), B(1,6), C(9,2), D(7,-2)
2. der er alt der allerede står i opgaven
Svar #7
05. maj 2021 af PeterValberg
gør samme for -2a+3b og undersøg om de to vektorer er ortogonale
#7
gør samme for -2a+3b og undersøg om de to vektorer er ortogonale
Hvilken formel bruge du, og hvorfor ganger du med 4?
Tak
Svar #10
05. maj 2021 af PeterValberg
#8 fordi der står 4 GANGE vektor a
læser du ikke dine opgavetekster?
Svar #11
05. maj 2021 af peter lind
#6
AB = 1, 6),- (-1, 2)= (-2, 4) BC = (9, 2) - (1,6) = (8, 4) AB·BC = (-2, 4)· (8, 4) = 0
De andre regnes tilsvarende
Du ka også i stedet bevise at modstående sider er parallelle
Lav evt. en tegning
#11#6
AB = 1, 6),- (-1, 2)= (-2, 4) BC = (9, 2) - (1,6) = (8, 4) AB·BC = (-2, 4)· (8, 4) = 0
De andre regnes tilsvarende
Du ka også i stedet bevise at modstående sider er parallelle
Lav evt. en tegning
Hej Peter,
kan du fortælle mig hvad de andre koordinater er? ikke udregningerne, kun hvilke koordinater det er?
Svar #13
05. maj 2021 af peter lind
BC·CD og CD·DE
Det sidste hjørne A kan du også regne på, men er ikke nødvendig, da summen af vinklerne i en firkant er 360º
#13BC·CD og CD·DE
Det sidste hjørne A kan du også regne på, men er ikke nødvendig, da summen af vinklerne i en firkant er 360º
Jeg laver nok en fejl et sted, men BC*CD får jeg til 16 eller -16 i skalarprodukt
#14#13BC·CD og CD·DE
Det sidste hjørne A kan du også regne på, men er ikke nødvendig, da summen af vinklerne i en firkant er 360º
Jeg laver nok en fejl et sted, men BC*CD får jeg til 16 eller -16 i skalarprodukt
Mener du ikke CD*DA og ikke CD*DE?
Svar #17
05. maj 2021 af peter lind
#15 BC = (9, 2) - (1,6) = (8, -4) CD = (7,-2) - (9, 2) = (-2, -4) BC·CD = ( 8, -4) (-2, -4) = -16 + 16 = 0
-
Svar #18
06. maj 2021 af peter lind
Beklager. Der er fejl i #11
AB = (1, 6),- (-1, 2)= (2, 4)
BC = (9, 2) - (1,6) = (8, -4)
Skriv et svar til: Vektorer spørgsmål?
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.