Matematik

Fartøjer - Vektorer

15. maj 2021 af qetzay - Niveau: B-niveau

Hej. Jeg har virkelig problemer med denne opgave er der nogen der kan hjælpe?

Spørgsmålet lyder:

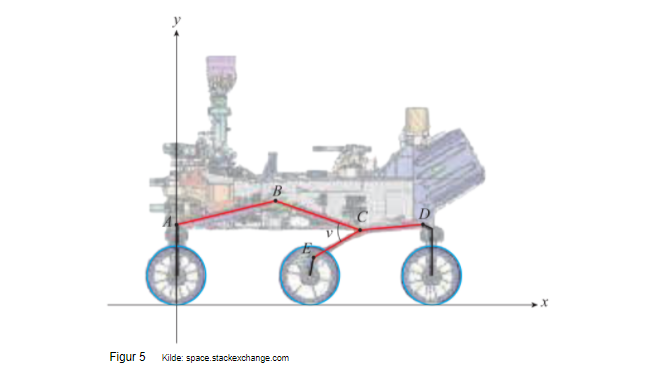
Hjulene er cirkelformede med en diameter på 520 mm, og det midterste hjul på figur 5 har centrum i punktet (1160 ; 260): Bestem, enten ved en grafisk konstruktion eller ved beregning, den korteste afstand fra stangen mellem B og C til centrum af det midterste hjul.

Yderligere information: Figur 5 viser en illustration af Curiosity indlagt i et koordinatsystem. Hjulophænget består blandt andet af nogle stænger, der kan beskrives som fire linjestykker tegnet med rødt på figur 5. Koordinaterne til punkterne, der afgrænser linjestykkerne, er givet ved A(0 ; 705), B(870 ; 910), C(1620 ; 645), D(2150 ; 710) og E(1190 ; yE). Alle mål er i millimeter, og yE blev bestemt i spørgsmål a).

Hvordan kan jeg med hjælp af beregning, bestemme den korteste afstand fra stangen mellem B og C til centrum af det midterste hjul?

Vedhæftet fil: opg 1 - 5.PNG

Brugbart svar (0)

Svar #1
15. maj 2021 af peter lind

Brugbart svar (0)

Svar #2
15. maj 2021 af peter lind

Ved beregning:

Find ligningerne fo en linjerne gennem BC og linjen, der er vinkelret på den og går gennem hjulets centrum. Der hvor de skærer hinanden er punktet,på BC, der mindst afstand til hjulets midte.

Hvis du kender formlen for afstanden fra et punkt på en linje, kan du også bruge den. Det er noget lettere

Svar #3
15. maj 2021 af qetzay

#2
Ved beregning:

Find ligningerne fo en linjerne gennem BC og linjen, der er vinkelret på den og går gennem hjulets centrum. Der hvor de skærer hinanden er punktet,på BC, der mindst afstand til hjulets midte.

Hvis du kender formlen for afstanden fra et punkt på en linje, kan du også bruge den. Det er noget lettere

Vil det sige afstandsformlen? Fordi det har jeg gjort. Ved bare ikke helt hvad jeg så skal efter?

Vedhæftet fil:hjælp matematik vektorer.PNG

Svar #4
15. maj 2021 af qetzay

#2
Ved beregning:

Find ligningerne fo en linjerne gennem BC og linjen, der er vinkelret på den og går gennem hjulets centrum. Der hvor de skærer hinanden er punktet,på BC, der mindst afstand til hjulets midte.

Hvis du kender formlen for afstanden fra et punkt på en linje, kan du også bruge den. Det er noget lettere

Hvad er formlen til at finde forskriften ud for 2 punkter? Fordi vi kender jo i forvejen punkterne for B og C...

Brugbart svar (0)

Svar #5
15. maj 2021 af peter lind

Hvad mener du ?

Brugbart svar (0)

Svar #6
15. maj 2021 af Eksperimentalfysikeren

Der er mere end én afstandsformel. Den du nævner er afstanden mellem to punkter.

Du kan finde ligningen (ax+by+c=0) for linien gennem B og C ved at finde vektoren BC. Tag dens tværvektor. Tværvektorens koordinater er

$\begin{pmatrix} a\\ b \end{pmatrix}$

Værdien af c finder du ved at indsætte koordinaterne til B eller C. Afstanden til E er så:

$dist = \frac{a\cdot x_{E} + b\cdot y_{E}+c}{\sqrt{a^{2}+b^{2}}}$

Svar #7
15. maj 2021 af qetzay

#6
Der er mere end én afstandsformel. Den du nævner er afstanden mellem to punkter.

Du kan finde ligningen (ax+by+c=0) for linien gennem B og C ved at finde vektoren BC. Tag dens tværvektor. Tværvektorens koordinater er

$\begin{pmatrix} a\\ b \end{pmatrix}$

Værdien af c finder du ved at indsætte koordinaterne til B eller C. Afstanden til E er så:

$dist = \frac{a\cdot x_{E} + b\cdot y_{E}+c}{\sqrt{a^{2}+b^{2}}}$

Sådan her, right??

Vedhæftet fil:vektor BC.PNG

Brugbart svar (0)

Svar #8
15. maj 2021 af Eksperimentalfysikeren

Det ser rigtigt ud.

PS. Jeg glemte, at der formlen for afstanden skal tages nummerisk værdi til slut på højre side af lighedstegnet.

$dist = |\frac{a\cdot x_{E} + b\cdot y_{E}+c}{\sqrt{a^{2}+b^{2}}}|$

Svar #9
15. maj 2021 af qetzay

#8
Det ser rigtigt ud.

PS. Jeg glemte, at der formlen for afstanden skal tages nummerisk værdi til slut på højre side af lighedstegnet.

$dist = |\frac{a\cdot x_{E} + b\cdot y_{E}+c}{\sqrt{a^{2}+b^{2}}}|$

Kan du uddybe lidt? ahahha har lidt svært ved at forstå det

Svar #10
15. maj 2021 af qetzay

#8
Det ser rigtigt ud.

PS. Jeg glemte, at der formlen for afstanden skal tages nummerisk værdi til slut på højre side af lighedstegnet.

$dist = |\frac{a\cdot x_{E} + b\cdot y_{E}+c}{\sqrt{a^{2}+b^{2}}}|$

Har bare lidt svært ved at se hvor man skal indsætte de forskellige punkter i formlen hahahaha

Svar #11
16. maj 2021 af qetzay

#8
Det ser rigtigt ud.

PS. Jeg glemte, at der formlen for afstanden skal tages nummerisk værdi til slut på højre side af lighedstegnet.

$dist = |\frac{a\cdot x_{E} + b\cdot y_{E}+c}{\sqrt{a^{2}+b^{2}}}|$

Kunne du uddybe? ^.^ Det ville være en stor hjælp

Svar #12
16. maj 2021 af qetzay

#8
Det ser rigtigt ud.

PS. Jeg glemte, at der formlen for afstanden skal tages nummerisk værdi til slut på højre side af lighedstegnet.

$dist = |\frac{a\cdot x_{E} + b\cdot y_{E}+c}{\sqrt{a^{2}+b^{2}}}|$

Er det her rigtigt? Er helt i tvivl om hvor de forskellige punkter skal sættes ind i formlen.... ;I

Vedhæftet fil:dist formel.PNG

Brugbart svar (0)

Svar #13
16. maj 2021 af ringstedLC

Du har to distanceformler (se FS), der bruges afhængigt af ligningsformen for linjen:

$\begin{align*} \textup{I}:\textup{dist}(P,l) &= \frac{\left | a\cdot x_1+b-y_1 \right |}{\sqrt{a^2+1}}\;,\;P=(x_1,y_1)\;,\;l:y=a\cdot x+b \\ \textup{II}:\textup{dist}(P,l) &= \frac{\left | a\cdot x_1+b\cdot y_1+c \right |}{\sqrt{a^2+b^2}}\;,\;P=(x_1,y_1)\;,\;l:a\cdot x+b\cdot y+c=0 \end{align*}$

#12. Nej. Du har taget ligningsformen fra "I" og brugt "II". Men a og b er jo ikke de samme størrelser i de to former.

Svar #14
16. maj 2021 af qetzay

#13
Du har to distanceformler (se FS), der bruges afhængigt af ligningsformen for linjen:

$\begin{align*} \textup{I}:\textup{dist}(P,l) &= \frac{\left | a\cdot x_1+b-y_1 \right |}{\sqrt{a^2+1}}\;,\;P=(x_1,y_1)\;,\;l:y=a\cdot x+b \\ \textup{II}:\textup{dist}(P,l) &= \frac{\left | a\cdot x_1+b\cdot y_1+c \right |}{\sqrt{a^2+b^2}}\;,\;P=(x_1,y_1)\;,\;l:a\cdot x+b\cdot y+c=0 \end{align*}$

#12. Nej. Du har taget ligningsformen fra "I" og brugt "II". Men a og b er jo ikke de samme størrelser i de to former.

Er helt lost... Har virkelig svært ved at forstå hvad der skal inde i formlen...

Brugbart svar (0)

Svar #15
16. maj 2021 af peter lind

For det første (-0,35)² = 0,35²

for det andet

Du skriver intet sted hvad du har fundet ligningen til

hvis du har fundet linjens ligning på formen ax+by + c = 0 skal du bruge formen

d= |ax+by+c|/kvrod(a²+b²)

Hvis du har brugt linjens ligning på formen

y = ax+b <=> ax-y + b skal du sætte b = -1 i ligningen ovenfor

Brugbart svar (0)

Svar #16
16. maj 2021 af ringstedLC

#14: efter bare 5 min...

Du har, efter hvad jeg kan se, fundet linjens ligning ved at konstrure og så fået den på ligningsformen i "I":

$\begin{align*} l:y &= -0.35x+1217.4 \\ C_{\textup{hjul}}=F &= ({\color{Red} 1160},{\color{Red} 260}) \\ \textup{I}:\textup{dist}(F,l) &= \frac{\left |a\cdot x_F+b-y_F \right |}{\sqrt{a^2+1}} \\&= \frac{\left |-0.35\cdot 1160+1217.4-260 \right |}{\sqrt{(-0.35)^2+1}} \end{align*}$

Men pga. koordinaternes størrelse og det ringe antal decimaler i linjens ligning, bliver ligningen for afrundet. Brug eksakte værdier i mellemregninger!

$\begin{align*} \overrightarrow{BC}=\vec{r}_l &= \binom{1620-870}{645-910} \\ \widehat{\vec{r}_l}=\vec{n}_l &= \binom{-\left (645-910 \right )}{1620-870}=\binom{a}{b} \\ l:a\cdot \left (x-x_B \right )+b\cdot \left ( y-y_B \right ) &= 0\;,\;(x_B,y_B)=B \\ a\cdot x+b\cdot y+\underset{c}{\underbrace{\left (-a\cdot x_B-b\cdot y_B \right )}} &= 0 \\ \textup{II}:\textup{dist}(F,l) &= \frac{\left |a\cdot {\color{Red} 1160}+b\cdot {\color{Red} 260}+c \right |}{\sqrt{a^2+1}} \end{align*}$

Svar #17
16. maj 2021 af qetzay

Jaa okay

Vedhæftet fil:lignings ligning 2.PNG

Svar #18
16. maj 2021 af qetzay

#17
Jaa okay

Hov glem det jeg har vedhæft. Den er ikke relevant.

Svar #19
16. maj 2021 af qetzay

Skal finde y = ax+by+c=0

Svar #20
16. maj 2021 af qetzay

#16
#14: efter bare 5 min...

Du har, efter hvad jeg kan se, fundet linjens ligning ved at konstrure og så fået den på ligningsformen i "I":

$\begin{align*} l:y &= -0.35x+1217.4 \\ C_{\textup{hjul}}=F &= ({\color{Red} 1160},{\color{Red} 260}) \\ \textup{I}:\textup{dist}(F,l) &= \frac{\left |a\cdot x_F+b-y_F \right |}{\sqrt{a^2+1}} \\&= \frac{\left |-0.35\cdot 1160+1217.4-260 \right |}{\sqrt{(-0.35)^2+1}} \end{align*}$

Men pga. koordinaternes størrelse og det ringe antal decimaler i linjens ligning, bliver ligningen for afrundet. Brug eksakte værdier i mellemregninger!

$\begin{align*} \overrightarrow{BC}=\vec{r}_l &= \binom{1620-870}{645-910} \\ \widehat{\vec{r}_l}=\vec{n}_l &= \binom{-\left (645-910 \right )}{1620-870}=\binom{a}{b} \\ l:a\cdot \left (x-x_B \right )+b\cdot \left ( y-y_B \right ) &= 0\;,\;(x_B,y_B)=B \\ a\cdot x+b\cdot y+\underset{c}{\underbrace{\left (-a\cdot x_B-b\cdot y_B \right )}} &= 0 \\ \textup{II}:\textup{dist}(F,l) &= \frac{\left |a\cdot {\color{Red} 1160}+b\cdot {\color{Red} 260}+c \right |}{\sqrt{a^2+1}} \end{align*}$

Jeg har fået beregnet tværvektoren. Jeg er bare stadigvæk i tvivl om hvor de forskellige koordinater skal indsættes i formlen. hvad er $x_B$ helt nøjagtigt? er det de 1160? og $y_B$ så er de 260?
Og mht til beregning af c så vi enige i at -a vil så være -0,35 og b er så 1217,4 right? så det bare lige $x_B$ og $y_B$ som jeg ikke helt forstår hvad er? ;// er virkelig forvirret og jeg undskylder for at bruge meget af din tid. Har bare svært ved at forstå det.

Vedhæftet fil:Lignings ligning.PNG

Forrige 1 2 Næste

Der er 30 svar til dette spørgsmål. Der vises 20 svar per side. Spørgsmålet kan besvares på den sidste side. Klik her for at gå til den sidste side.