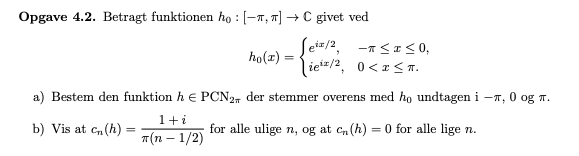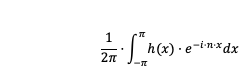Matematik

Funktioner, lige, ulige

14. juni 2021 af K22 - Niveau: Universitet/Videregående

Hej. Jeg kunne godt bruge noget hjælp til disse opgaver. På forhånd tak.

Vedhæftet fil: Skærmbillede 2021-06-14 kl. 22.35.50.png

Brugbart svar (1)

Svar #1
16. juni 2021 af AskTheAfghan

(a) Du skal bestemme en stykkevist kontinuert og normaliseret funktion h på [−π, π], sådan at h = h₀ på (−π, π)\{0}.

Svar #2
16. juni 2021 af K22

Kan du uddybe? Er helt fortabt i det her:(

Brugbart svar (0)

Svar #3
17. juni 2021 af Soeffi

#0.

Svar #4
20. juni 2021 af K22

Kan det passe, at jeg skal løse følgende integral i b)? Hvis det er rigtigt, hvad skal jeg så sætte ind på h(x)'s plads? Jeg har lavet delopgave a).

Vedhæftet fil:Skærmbillede 2021-06-20 kl. 21.52.11.png

Brugbart svar (0)

Svar #5
20. juni 2021 af Soeffi

#4. Indsætter billede...

Brugbart svar (0)

Svar #6
22. juni 2021 af Moderatoren

Fortsat her: https://www.studieportalen.dk/forums/thread.aspx?id=2018116#2018117

Brugbart svar (0)

Svar #7
22. juni 2021 af Soeffi

#0. Du ved vel ikke hvad $PCN_{2\pi}$ betyder?

Brugbart svar (0)

Svar #8
22. juni 2021 af Soeffi

#4... Jeg har lavet delopgave a).

Må jeg spørge, hvad du fik?

Svar #9
22. juni 2021 af K22

Jeg fik en stykvis funktion. Det tager desværre lang tid at sætte det hele ind i indlægget, men det er heller ikke den opgave, jeg har brug for hjælp til.

Brugbart svar (0)

Svar #10
22. juni 2021 af Soeffi

#9. Jo, men vi er nød til at kende h(x) for at kunne beregne Fourier-koefficienterne, og det kan vi ikke, da ingen ved, hvad der menes med PCN_2π!

Brugbart svar (0)

Svar #11
23. juni 2021 af Soeffi

#0. Lad os sige, at du ønsker at bestemme...

$\frac{1}{2\pi }\cdot \int_{-\pi}^{\pi}e^{i\cdot x/2} \cdot e^{-i\cdot n\cdot x}\;dx$

Teknikken er ikke særlig svær. Du får:

$\frac{1}{2\pi }\cdot \int_{-\pi}^{\pi}e^{i\cdot x/2} \cdot e^{-i\cdot n\cdot x}\;dx=\frac{1}{2\pi }\cdot \int_{-\pi}^{\pi}e^{i\cdot x/2-i\cdot n\cdot x}\;dx=\frac{1}{2\pi }\cdot \int_{-\pi}^{\pi}e^{i\cdot x(1/2-n)}\;dx=$

$\frac{1}{2\pi }\cdot \frac{1}{i\cdot (1/2-n)} \left [ e^{i\cdot x\cdot (1/2-n)} \right ]_{-\pi}^{\pi}=\frac{i}{2\pi(n-1/2)} \left [ e^{i\cdot \pi\cdot (1/2-n)} -e^{-i\cdot \pi\cdot (1/2-n)} \right ]=$

$\frac{i}{2\pi(n-1/2)} \left [ 2\cdot i\cdot sin(\frac{\pi}{2}-n\cdot \pi ) \right ]=$

$\frac{ -1}{\pi(n-1/2)} \left [sin(\frac{\pi}{2}-n\cdot \pi ) \right ]=$

$\frac{ -1}{\pi(n-1/2)} \cdot (-1)^n=\frac{ (-1)^{n+1}}{\pi(n-1/2)}$

Brugbart svar (0)

Svar #12
23. juni 2021 af Soeffi

#11. En anden teknik:...

$e^{i\cdot \pi\cdot (1/2-n)} -e^{-i\cdot \pi\cdot (1/2-n)} =$

$e^{i\cdot \pi/2} \cdot (e^{-i\cdot \pi})^n -e^{-i\cdot \pi/2} \cdot (e^{i\cdot \pi})^n=$

$\\(cos(\pi/2)+i\cdot sin(\pi/2)) \cdot (cos(-\pi)+i\cdot sin(-\pi))^n -$

$(cos(-\pi/2)+i\cdot sin(-\pi/2)) \cdot (cos(\pi)+i\cdot sin(\pi))^n=$

$\\(0+i\cdot 1) \cdot (-1+i\cdot 0)^n -(0+i\cdot (-1)) \cdot (-1+i\cdot 0)^n=$

$i \cdot (-1)^n -(i\cdot (-1)) \cdot (-1)^n=$

$i \cdot (-1)^n +i \cdot (-1)^n=$

$2\cdot i\cdot (-1)^n$

Svar #13
24. juni 2021 af K22

Dette er h(x). Hvordan skal jeg så lave b)?

Vedhæftet fil:Skærmbillede 2021-06-24 kl. 08.32.58.png

Brugbart svar (0)

Svar #14
24. juni 2021 af Soeffi

#13...Jeg tror, at du mener:

$h(x)=\left\{\begin{matrix} e^{i\cdot x/2}\;\;\;-\pi<x<0 \\ \frac{i+1}{2}\;\;\;\;\;\;\;x=0 \;\;\;\;\;\;\;\;\;\; \\ i e^{i\cdot x/2}\;\;\;\;0<x<\pi\;\;\; \\ \frac{i-1}{2}\;\;\;\;\;\;\;\;x=\{-\pi ,\pi \} \end{matrix} \right.$

Du har at...

$c_n(h)=\frac{1}{2\pi }\cdot \int_{-\pi}^{\pi}h(x) \cdot e^{-i\cdot n\cdot x}\;dx=$

dette deles op...

$\frac{1}{2\pi }\cdot \int_{-\pi}^{0}e^{ix/2} \cdot e^{-i n x}\;dx+\frac{1}{2\pi }\cdot \int_{0}^{\pi}ie^{ix/2} \cdot e^{-i n x}\;dx=$

eksponenter trækkes sammen...

$\frac{1}{2\pi }\cdot \int_{-\pi}^{0}e^{i(1/2- n )\cdot x} \;dx+\frac{i}{2\pi }\cdot \int_{0}^{\pi}e^{i(1/2-n )\cdot x} \;dx=$

man finder stamfunktionen og indsætter grænser...

$\frac{1}{2\pi }\cdot \left [ \frac{e^{i(1/2- n )\cdot 0}-e^{i(1/2- n )\cdot (-\pi)}}{i(1/2- n ) } \right ]+\frac{i}{2\pi }\cdot \left [ \frac{e^{i(1/2- n )\cdot \pi}-e^{i(1/2- n )\cdot 0}}{i(1/2- n ) } \right ]=$

fælles faktorer sættes udenfor...

$\frac{1}{2\pi \cdot i(1/2- n ) }\cdot \left ( 1-e^{-i(1/2- n )\cdot \pi} +i\cdot \left [ e^{i(1/2- n )\cdot \pi}-1 \right ] \right )=$

omskriv eksponentialfunktioner til produktform...

$\frac{1}{2\pi \cdot i(1/2- n ) }\cdot \left (1-e^{-i\pi/2}\cdot (e^{i\pi})^n +i\cdot \left [ e^{i\pi/2}\cdot (e^{-i\pi})^n-1 \right ] \right )=$

indsæt Eulers formel...

$\frac{1}{2\pi \cdot i(1/2- n ) }\cdot \left (1-i\cdot sin(-\pi/2)\cdot (cos(\pi))^n +i\cdot \left [ i\cdot sin(\pi/2)\cdot (cos(-\pi))^n-1 \right ] \right )=$

indsæt værdier af trigonomiske funktioner...

$\frac{1}{2\pi \cdot i(1/2- n ) }\cdot \left (1- (-1)^n+i\cdot ((-1)^n -1) \right )=$

gang tæller og nævner med i...

$\frac{1}{2\pi \cdot (1/2- n ) }\cdot \left ( (-1)^n -1+i((-1)^n -1) \right )$

Brugbart svar (0)

Svar #15
25. juni 2021 af Soeffi

#14. Dvs....

$a)\;h(x)=\left\{\begin{matrix} e^{i\cdot x/2}\;\;\;-\pi<x<0 \\ \frac{i+1}{2}\;\;\;\;\;\;\;x=0 \;\;\;\;\;\;\;\;\;\; \\ i e^{i\cdot x/2}\;\;\;\;0<x<\pi\;\;\; \\ \frac{i-1}{2}\;\;\;\;\;\;\;\;x=\{-\pi ,\pi \} \end{matrix} \right.$

$b)\;c_n(h)=\frac{1}{2\pi \cdot (1/2- n ) }\cdot \left ( (-1)^n -1+i((-1)^n -1) \right )$

Hvoraf følger:

$c_n(h)=\frac{1}{2\pi \cdot (1/2- n ) }\cdot\left\{\begin{matrix} (-1)^1 -1+i((-1)^1 -1) \;\;n \;ulige\; \\ (-1)^2 -1+i((-1)^2 -1) \;\;n \;lige \;\;\; \end{matrix} \right. \Rightarrow$

$c_n(h)=\frac{1}{(-2)\cdot \pi \cdot (n-1/2) }\cdot\left\{\begin{matrix} (-2)\cdot (1+i)\;\;n \;ulige \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n \;lige \; \end{matrix} \right. \Rightarrow$

$c_n(h)=\left\{\begin{matrix} \frac{ 1+i}{\pi \cdot (n-1/2 ) }\;\;\;n \;ulige \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;n \;lige \;\; \end{matrix} \right.$

Skriv et svar til: Funktioner, lige, ulige

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.