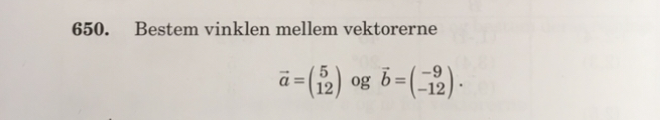Matematik

Vinkler

04. november 2021 af javannah5 - Niveau: A-niveau

Kan nogle hjælpe mig med opgaven? Hvilken formel skal jeg bruge?

Vedhæftet fil: 6F13100C-670D-431C-97DA-55E3DFC6F77A.jpeg

Brugbart svar (0)

Svar #1
04. november 2021 af inaktiv

https://www.webmatematik.dk/lektioner/matematik-b/vektorer-i-2d/vinkel-mellem-vektorer
^^^^
Det første resultat der kommer frem når man søger på vinklen mellem to vektorer :)

Brugbart svar (0)

Svar #2
04. november 2021 af SuneChr

I virkeligheden er det definitionen på cos af en vinkel.
cos af vinklen mellem to enhedsvektorer a/|a| og b/|b|
er enhedsvektorernes skalære produkt.

Brugbart svar (0)

Svar #3
04. november 2021 af PeterValberg

Se eventuelt video nr. 11 på denne videoliste < LINK >

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #4
04. november 2021 af Eksperimentalfysikeren

#2 Det er ikke definitionen på cos(v). Sin(v) og cos(v) defineres ud fra enhedscirklen.De er faktisk ældre end vektorregningen.

Brugbart svar (0)

Svar #5
04. november 2021 af mathon

... men #0
$\small \begin{array}{lllll} v=\cos^{-1}\left ( \frac{\overrightarrow{a}\cdot \overrightarrow{b}}{\left | \overrightarrow{a} \right |\cdot \left | \overrightarrow{b} \right |} \right )\\\\ v_{spids}=\cos^{-1}\left ( \frac{\left |\overrightarrow{a}\cdot \overrightarrow{b} \right |}{\left | \overrightarrow{a} \right |\cdot \left | \overrightarrow{b} \right |} \right ) \end{array}$

Svar #6
04. november 2021 af javannah5

Hvordan regner man det her ud i tnspire?

Vedhæftet fil:image.jpg

Brugbart svar (0)

Svar #7
04. november 2021 af mathon

#6
$\small v=\cos^{-1}\left ( \frac{\textup{dotP}\left ( \begin{bmatrix} 5\\12 \end{bmatrix},\begin{bmatrix} -9\\ -12 \end{bmatrix} \right )}{\textup{norm}\begin{bmatrix} 5\\12 \end{bmatrix}\cdot \textup{norm}\begin{bmatrix} -9\\ -12 \end{bmatrix}} \right )$

Svar #8
04. november 2021 af javannah5

Af hvad jeg er nået frem til rigtigt?

Vedhæftet fil:image.jpg

Brugbart svar (0)

Svar #9
04. november 2021 af mathon

Nej
længden af vektor b er forkert beregnet.

Brugbart svar (0)

Svar #10
04. november 2021 af mathon

$\small \small v_{spids}=\cos^{-1}\left ( \frac{\textup{abs}\left (\textup{dotP}\left ( \begin{bmatrix} 5\\12 \end{bmatrix},\begin{bmatrix} -9\\ -12 \end{bmatrix} \right ) \right )}{\textup{norm}\begin{bmatrix} 5\\12 \end{bmatrix}\cdot \textup{norm}\begin{bmatrix} -9\\ -12 \end{bmatrix}} \right )$

Svar #11
04. november 2021 af javannah5

#7
Jeg regnede det på tnspire. Er det rigtigt?

Vedhæftet fil:image.jpg

Brugbart svar (0)

Svar #12
04. november 2021 af mathon

$\small \small \small v_{spids}=\cos^{-1}\left ( \frac{\textup{abs}\left (\textup{dotP}\left ( \begin{bmatrix} 5\\12 \end{bmatrix},\begin{bmatrix} -9\\ -12 \end{bmatrix} \right ) \right )}{\textup{norm}\begin{bmatrix} 5\\12 \end{bmatrix}\cdot \textup{norm}\begin{bmatrix} -9\\ -12 \end{bmatrix}} \right )=14.25\degree$

efter tryk på ctrl + <enter>

Skriv et svar til: Vinkler

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.