INTEGRATION vha. SUBSTITUTION - Matematik

Brugbart svar (1)

Svar #1
03. juli 2022 af oppenede

I begge to kan du multiplicere med en konstant under integraltegnet sådan at du får et produkt med den indres afledede, f.eks.:

∫√(2x+5)dx = 1/2·∫2√(2x+5)dx

Hvor der er kompenseret ved at dividere med 2 uden for integraltegnet, hvilket man kan da konstante faktorer kommuterer med integration.

Svar #2
03. juli 2022 af 94Amalie

Det har jeg lidt svært ved at forstå.

Altså, jeg er med på at sætningen gælder, hvis jeg omskriver som du siger og ganger med 2 under integraltegnet, og derefter dividerer med 1/2 uden for integraltegnet for at det går lige op - og så stemmer pengene. Men det behøver jeg vel ikke? Metoden vil jo stadig virke, selv hvis ikke jeg gør det.

Håber du gider at uddybe og tak for hjælpen :)

Brugbart svar (1)

Svar #3
03. juli 2022 af jl9

Fordi vi gerne vil have det til at stå på formen:

$\int{ f(g(x)) \cdot g'(x) } dx$

Så er $f(t)=\sqrt{t}$ og $g(x)=2x+5$ i dit eksempel.

Hvad er så $g'(x)$ ?

Brugbart svar (1)

Svar #4
03. juli 2022 af mathon

Svar #5
03. juli 2022 af 94Amalie

Hvad er så g'(x)?

Den er $dt/dx = 2$

Men jeg kan godt løse ∫√(2x+5)dx vha. substitutionsmetoden, UDEN at jeg skal omskrive opgaven.

Det jeg ikke forstår er, at opgaven ikke opfylder de kriterier, som står på formlen. Der bliver ikke ganget med den indre funktions differentialkvotienten.

Hvad er det som jeg ikke forstår? ....

Vedhæftet fil:studieportalen.png

Brugbart svar (1)

Svar #6
03. juli 2022 af mathon

$\small \begin{array}{llllll}&& \int \sqrt{2x+5}\,\mathrm{d}x \\\textup{her s\ae ttes:}\\&&t=2x+5\quad\textup{og dermed}\quad \frac{1}{2}\mathrm{d}t=\mathrm{d}x\\ \textup{dvs}\\&&\int \sqrt{t}\cdot \frac{1}{2}\mathrm{d}t=\frac{1}{2}\cdot \int \sqrt{t}\,\mathrm{d}t=\frac{1}{2}\cdot \frac{2}{3}\cdot t^{\frac{3}{2}}+k=\frac{1}{3}\cdot t^{\frac{3}{2}}+k=\\\\&& \frac{1}{3}\cdot \left ( 2x+5 \right )^{\frac{3}{2}}+k \end{array}$

Svar #7
03. juli 2022 af 94Amalie

Hej mathon, det er ikke metodeanvendelsen jeg ikke forstår, men teorien bag det. Prøv at læse #5.

Tak for hjælpen :)

Brugbart svar (1)

Svar #8
03. juli 2022 af mathon

men
$\small \int \sqrt{2x+5}\,\mathrm{d}x=\frac{1}{2}\cdot \int \sqrt{2x+5}\cdot 2\mathrm{d}x$

Brugbart svar (1)

Svar #9
03. juli 2022 af mathon

$\small \begin{array}{lllllll}&& \int \left ( x^3+4 \right )^2\cdot x^2\mathrm{d}x=\frac{1}{3}\cdot \int \left ( x^3+4 \right )^2\cdot3 x^2\mathrm{d}x\\ \textup{her s\ae ttes:}\\&&t=x^3+4\quad\textup{og dermed}\quad \mathrm{d}t=3x^2\,\mathrm{d}x\\ \textup{dvs}\\&&\frac{1}{3}\cdot \int \left ( x^3+4 \right )^2\cdot3 x^2\mathrm{d}x=\frac{1}{3}\cdot \int t^2\cdot \mathrm{d}t=\frac{1}{3}\cdot \frac{1}{3}\cdot t^3+k=\\\\&& \frac{1}{9}\cdot \left (x^3+4 \right )^3+k \end{array}$

Brugbart svar (1)

Svar #10
04. juli 2022 af Anders521

#5 Du har ret i, at integralet ikke passer med skrivemåden , men du kan omskrive det:

$\small \int \sqrt{2x+5}\, \textup{d}x=\sqrt{2} \cdot \int \sqrt{x+\frac{5}{2}} \cdot 1\, \textup{d}x$

Her er og , hvor .

Brugbart svar (1)

Svar #11
04. juli 2022 af mathon

Når du anvender
$\small \begin{array}{llllll}&& \frac{\mathrm{d}t}{\mathrm{d}x}=2\Leftrightarrow 2\mathrm{d}x=\mathrm{d}t\\ \textup{er der - omend ikke noteret -}\\ \textup{"foretaget" en omskrivning:}\\&&\int \sqrt{2x+5}\cdot \underset{\left ( 2x+5 \right ){}'=g{\, }'(x)}{\mathbf{{\color{Red} \underbrace{2}}}}x\,\mathrm{d}x=\int \sqrt{t}\,\mathrm{d}t \end{array}$

Brugbart svar (1)

Svar #12
04. juli 2022 af mathon

korrektion:

Når du anvender
$\small \begin{array}{llllll}&&\\&&t=2x+5\\\\&&\frac{\mathrm{d}t}{\mathrm{d}x}=2\Leftrightarrow 2\mathrm{d}x=\mathrm{d}t\\ \textup{er der - omend ikke noteret -}\\ \textup{"t\ae nkt foretaget" en omskrivning:}\\&& \int (2x+5)\,\mathrm{d}x=\frac{1}{2}\cdot\int \sqrt{2x+5}\cdot \underset{\left ( 2x+5 \right ){}'=g{\, }'(x)}{\mathbf{{\color{Red} \underbrace{2}}}}x\,\mathrm{d}x=\int \sqrt{t}\,\mathrm{d}t \end{array}$

Svar #13
04. juli 2022 af 94Amalie

#12 Ahaa! Nu klikkede det.

Det giver mening. Tusind tak for hjælpen mathon :)

Brugbart svar (1)

Svar #14
04. juli 2022 af mathon

2. korrektion:

Når du anvender
$\small \begin{array}{llllll}&&\\&&t=2x+5\\\\&&\frac{\mathrm{d}t}{\mathrm{d}x}=2\Leftrightarrow 2\mathrm{d}x=\mathrm{d}t\\ \textup{er der - omend ikke noteret -}\\ \textup{"t\ae nkt foretaget" en omskrivning:}\\&& \int (2x+5)\,\mathrm{d}x=\frac{1}{2}\cdot\int \sqrt{2x+5}\cdot \underset{\left ( 2x+5 \right ){\, }'=g{\, }'(x)}{\mathbf{{\color{Red} \underbrace{2}}}}x\,\mathrm{d}x=\frac{1}{2}\cdot \int \sqrt{t}\,\mathrm{d}t \end{array}$

Svar #15
04. juli 2022 af 94Amalie

mathon, vil du ikke lige en sidste gang forklare mig, hvorfor jeg ikke får det samme resultat her:

Vedhæftet fil:sidste eksempel.png

Brugbart svar (1)

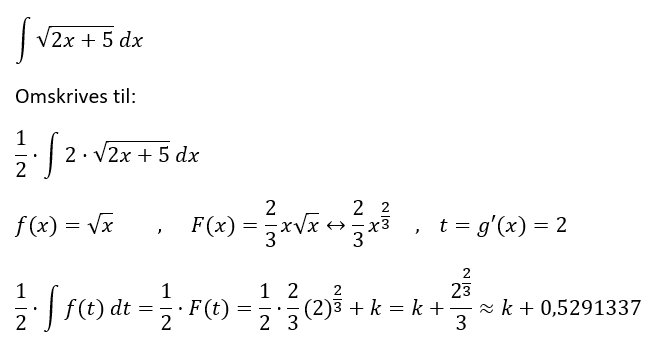
Svar #16
04. juli 2022 af mathon

#15

$\small \small \begin{array}{lllllll}\textup{for }x\geq -\frac{5}{2} \\\\\int \sqrt{2x+5}=\frac{1}{2}\cdot \int 2\cdot \sqrt{2x+5}\,\mathrm{d}x=\frac{1}{2}\cdot \int \sqrt{2x+5}\cdot 2\mathrm{d}x=\frac{1}{2}\cdot \int \sqrt{t}\,\mathrm{d}t=\\\\ \frac{1}{2}\cdot\left ( \frac{2}{3}\cdot t\cdot \sqrt{t} \right )+k=\left (\frac{1}{2}\cdot \frac{2}{3} \right )\cdot \left ( 2x+5 \right )\cdot \sqrt{2x+5}+k=\frac{1}{3}\cdot \left ( 2x+5 \right )^{\frac{3}{2}}+k \end{array}$

Din variabel smutter i sidste linje. (det ubestemte integral er en funktion og ikke en talværdi).

Svar #17
06. juli 2022 af 94Amalie

Okay så har jeg forfattet et par linjer om min udfordring - som jeg langt om længe har løst takket være jeres hjælp. Det er utroligt, at fagbøgerne er så dårlige til at uddybe disse nuancer, så man kan få en ordentlig forståelse for, hvordan det hele hænger sammen.

I er meget velkomne til at kommentere på, hvorvidt det jeg har fanget det rigtigt:

Se vedhæftet fil :)

Vedhæftet fil:finally.png

Brugbart svar (1)

Svar #18
06. juli 2022 af Anders521

#17 Der mangler oplysninger om integrationsmetoden. Integration ved substitution er mere end blot formlen Tilføj hvad der skal gælde for funktionerne og .

Brugbart svar (1)

Svar #19
07. juli 2022 af mathon

Krav:
   f(x) er kontinuert
   g(x) er er differentiabel med kontinuert afledet.
   g afbilder intervallet [a;b] ind i definitionsmængden for f
   såles at der kan opereres med sammensætningen
f(g(x)) i det nævnte interval.
   Med F betegnes stamfunktionen til f.

Brugbart svar (1)

Svar #20
07. juli 2022 af mathon

eventuelt:

$\small \int \sqrt{2x+5}\,\mathrm{d}x$

her sættes
$\small u=\sqrt{2x+5}\quad\textup{og dermed}\quad \frac{\mathrm{d} u}{\mathrm{d} x}=\frac{1}{\sqrt{2x+5}}\Leftrightarrow \mathrm{d}x=\sqrt{2x+5}\cdot \mathrm{d}u=u\cdot \mathrm{d}u$

hvoraf

$\small \int \sqrt{2x+5}\,\mathrm{d}x=\int u\cdot u\mathrm{d}u=\int u^2\,\mathrm{d}u=\frac{1}{3}\cdot u^3+k=\frac{1}{3}\cdot\left ( \sqrt{2x+5} \right )^3+k=$

$\small \frac{1}{3}\cdot \left (\left ( 2x+5 \right )^{\frac{1}{2}} \right )^3+k=\frac{1}{3}\cdot\left ( 2x+5 \right )^{\frac{3}{2}}+k$