Matematik

Integral og areal

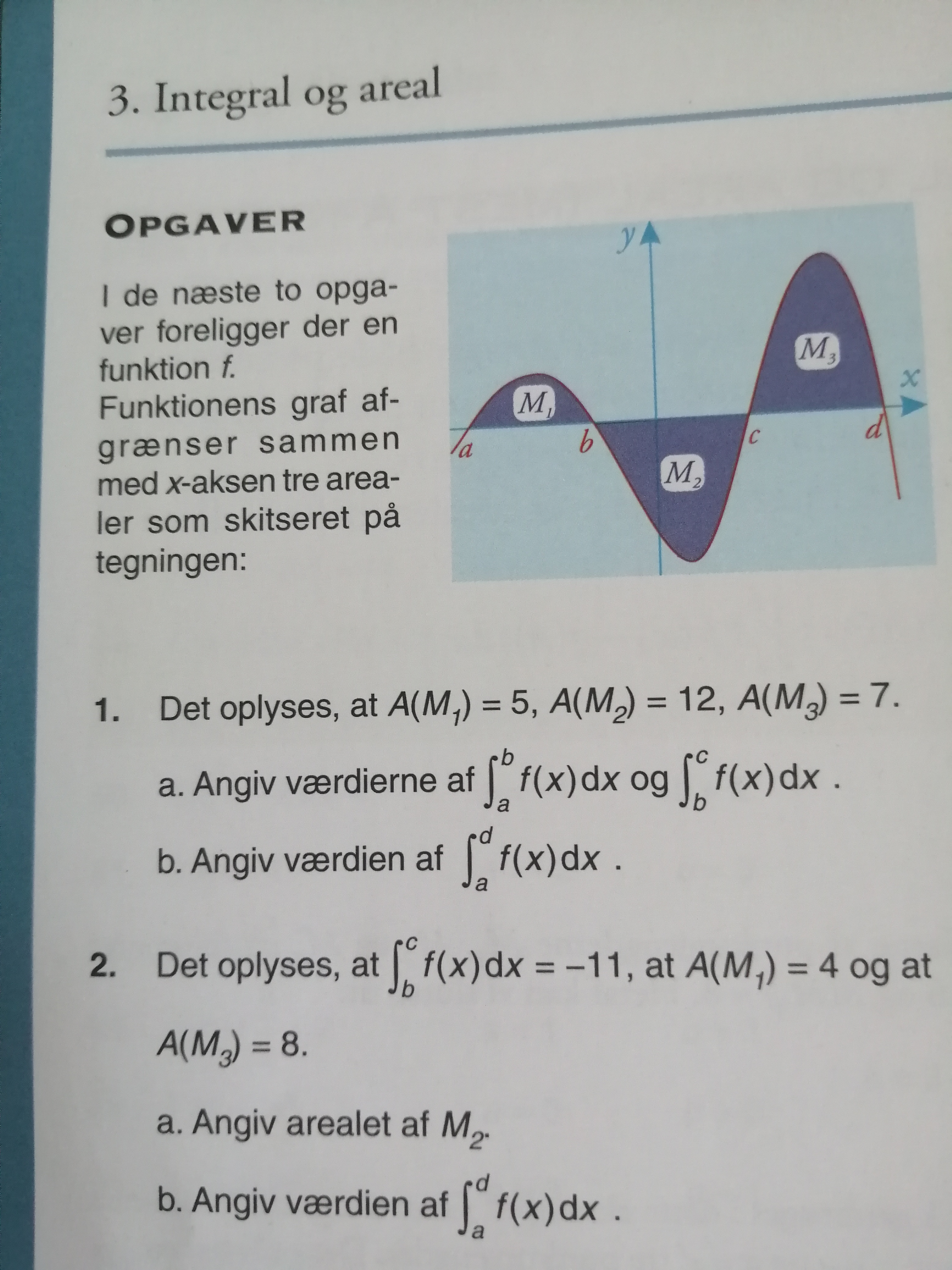
04. oktober 2022 af Anonym706 - Niveau: A-niveau

Det oplyses, at A(m₁) = 5, A(m₂) = 12, A(m₃) = 7

En skitse over grafen kan ses i vedhæftede samt opgaverne.

Det jeg ikke forstår er hvordan man kan vise reasultatet ved udregning? Jeg kan aflæse at svaret til a) er 5 og -12 men jeg kan ikke se hvordan man kan vise dette ved udregning.

Jeg har udregnet svaret til b)

Nogle der kan hjælpe? På forhånd, tak.

Vedhæftet fil: IMG_20221004_174415.jpg

Brugbart svar (0)

Svar #1
04. oktober 2022 af Anders521

#0 Det er ikke meningen, at arealerne skal udregnes.

Brugbart svar (0)

Svar #2
04. oktober 2022 af Stevenfeldt

A(m1)=5. Det betyder at

$\int_a^b f(x) dx=5$

osv. Du skal bare vise, at du ved hvad integralet beregner.

Brugbart svar (0)

Svar #3
04. oktober 2022 af ringstedLC

Brugbart svar (0)

Svar #4
04. oktober 2022 af ringstedLC

$\begin{align*}\textup{a)}\\ A(M_1)=\left | \int_{a}^{b}\!f(x)\,\mathrm{d}x \right | &= 5 \\ \Rightarrow \int_{a}^{b}\!f(x)\,\mathrm{d}x &= 5\;,\;f(x)\geq 0\;,\;a\leq x\leq b \\ A(M_3)=\left | \int_{c}^{d}\!f(x)\,\mathrm{d}x \right | &= 7 \\ \Rightarrow \int_{c}^{d}\!f(x)\,\mathrm{d}x &= 7\;,\;f(x)\geq 0\;,\;c\leq x\leq d \\ \textup{b)} \\A(M_2)=\left | \int_{b}^{c}\!f(x)\,\mathrm{d}x \right | &= 12 \\ \Rightarrow \int_{b}^{c}\!f(x)\,\mathrm{d}x &= -12\;,\;f(x)\leq 0\;,\;b\leq x\leq c \\ \int_{a}^{d}\!f(x)\,\mathrm{d}x &= \int_{a}^{b}\!f(x)\,\mathrm{d}x+\int_{b}^{c}\!f(x)\,\mathrm{d}x +\int_{c}^{d}\!f(x)\,\mathrm{d}x=... \end{align*}$

Brugbart svar (0)

Svar #5
04. oktober 2022 af ringstedLC

$\begin{align*} \textup{a)}\\A(M_2) &= \left | -11 \right |=...\\\textup{b)}\\&\textup{ som 1. b)} \end{align*}$

Skriv et svar til: Integral og areal

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.