Matematik
Modeller for udvikling i befolkningstal, Vejen til Matematik A2, Opgave 186, Side 167, (Knud Erik Nielsen og Esper Fogh)
I to modeller for udvikling i befolkningstal antager man, at befolkningstallet afhænger af tiden t på følgende måde:
2000
Model 1: f ( t ) = ------------------------
1 + 4 • e -0,5•t
Model 2 : f ( t ) = 400 • e-0,4 • t
a) Hvor stor er befolningen til t = 0 ?
Mit forsøg
Model 1:
2000
Model 1: f ( 0 ) = ------------------------ = 400
1 + 4 • e -0,5•0
Model 2: f( 0 ) = 400 • e-0,4 • 0 = 900
b) Hvor stor er væksthastigheden til tiden t ?
Mit forsøg
( 2000 )' • ( 1 + 4 • e -0,5 • t ) - 2000 • ( 1 + 4 • e -0,5 • t )'
Model 1: f '( t ) = -------------------------------------------------------------------------- =
( 1 + 4 • e -0,5•t )2
-2000 • ( -0,5 • 4 • e -0,5•t )
= ---------------------------------------
( 1 + 4 • e -0,5•t )2
4000 • e -0,5 • t
= ----------------------------------
( 1 + 4 • e -0,5•t )2
Bogens facit side 394 er følgende:
4000 • 1,6487t
Model 1 : f ' ( t ) = ------------------------------
( 1,6487t + 4)2
Mit spørgsmål er hvad gør jeg forkert ?
Svar #2
03. februar 2023 af StoreNord
Prøv at tegne din og bogens løsning i samme kordinatsystem. Måske er graferne ens, så begge dele er rigtige.
Svar #3
03. februar 2023 af StoreNord
Ja. Model 1 var ihvertfald rigtig.
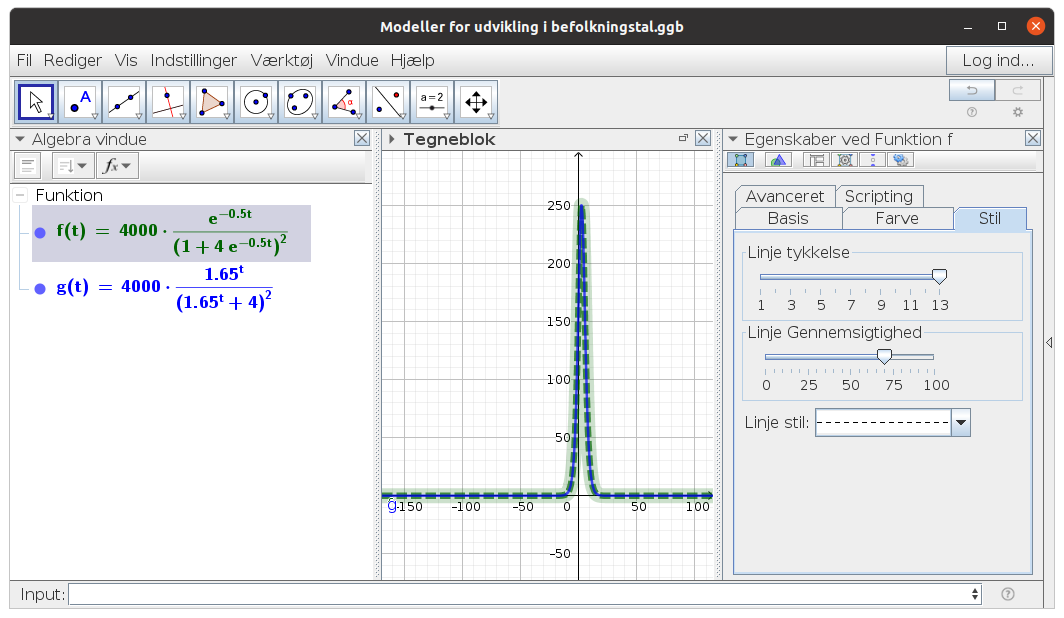
Svar #5
03. februar 2023 af ca10
Jeg brugte kvotientreglen da jeg bestemte væksthastigheden til tiden t for model 1, så det burde vel være udført rigtigt.
Mit spørgsmål er, hvordan kommer frem til
1,65t
f ' ( t ) = g ( t ) = 4000 • -----------------------
( 1,65t + 4 )2
Da jeg har ikke det program du har anvendt i svar #3.
Model 2: f ' ( t ) = (400 • e-0,4 • t + 500) ' = -160 e-0,4 • t
( Det samme som facitlisten )
Svar #6
03. februar 2023 af Anders521
#5 Mon ikke der er fejl i facit. Med dit resultat i #0
f'(t) = 4000·e -0,5·t/( 1 + 4·e-0,5·t )2
kan der foretages en omskrivning, hvor e-0,5·t = 1/e0,5·t = 1/(√e)t ≈ 1/1,64872t.
a) Tælleren til f' ændres fra 4000·e -0,5·t til 4000·1,64872-t. b) Nævneren til f' ændres fra 1 + 4·e-0,5·t til 1,64872t + 4
Således fås et omskrevet udtryk
f'(t) = 4000·1,64872-t/(1,64872t + 4)2
Svar #8
04. februar 2023 af ca10
Jeg har set nærmer på din omskrivning e-0,5·t = 1/e0,5·t = 1/(√e)t ≈ 1/1,64872t. for tallet e (også kaldet Eulers tal,opkaldt efter matematikeren Leonhard Euler) er et transcendent tal, der har denne afkortede og tilnærmede værdi på 2,7182818284590452353602.
√2,7182818284590452353602 = 1,6487212707 ≈ 1,6487
Så forstår jeg dit svar.
Jeg har anvendt TI - 89 Titanium og her anvendes ikke t men i stedet x og jeg har derefter gjort følgende:
Først tastes
d (f ) , x → df (x) tryk enter og svaret er Done
Dernæst tastes
2000
----------------------------------- → f ( x ) tryk enter og svaret er Done
(1 + 4 • e(-0,5 • x) ))
Til slut tastes:
d f ( x ) tryk enter og svaret er (der anvendes ikke komma men i stedet for symbolet for punktum er .) :
4000 • ( 1.6487 )x
-------------------------------------
(( 1.6487 )x + 4)2
Skriv et svar til: Modeller for udvikling i befolkningstal, Vejen til Matematik A2, Opgave 186, Side 167, (Knud Erik Nielsen og Esper Fogh)
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.








