Matematik

hjælp til opgave om volumen

19. marts 2023 af fjg5th - Niveau: A-niveau

hejsa allesammen, sidder fast i denne matematik opgave. håber der er nogen der kan hjælpe mig med de delopgaver og fortælle mig hvilken formel jeg skal bruge i a, b, c og d. se blandt andet selve vedhæftet fil. Tak på forhånd.

Vedhæftet fil: opgave 5.png

Brugbart svar (0)

Svar #1
19. marts 2023 af ringstedLC

Brugbart svar (1)

Svar #2
19. marts 2023 af mathon

Brug
   i øverste flade
   arealformlen:
      $\small T_\textup{enkelt trekant}=\frac{13^2}{2}\cdot \frac{\sin^2\left ( \frac{135\degree}{2} \right )}{\sin(45\degree)}$

$\small T_\textup{flade}=8\cdot \left (\frac{13^2}{2}\cdot \frac{\sin^2\left ( \frac{135\degree}{2} \right )}{\sin(45\degree)} \right )$

Brugbart svar (1)

Svar #3
19. marts 2023 af ringstedLC

$\begin{align*} V &= \pi\,h\cdot \bigl(R^2-r^2) \end{align*}$

Svar #4
19. marts 2023 af fjg5th

jeg har diameter? hvad er store R?

Brugbart svar (0)

Svar #5
19. marts 2023 af Sofia0294

Brugbart svar (1)

Svar #6
19. marts 2023 af mathon

Nej.

$\small A_\textup{ring}=h\cdot \pi\cdot \left ( R^2-r^2 \right )=h \cdot \pi\left ( \left (\frac{D}{2} \right )^2-\left ( \frac{d}{2} \right )^2\right )$

Brugbart svar (0)

Svar #7
19. marts 2023 af Sofia0294

Svar #8
19. marts 2023 af fjg5th

tak skal du have, nu forstår jeg. hvilke formel skal bruges i b,c og d?

Brugbart svar (0)

Svar #9
19. marts 2023 af mathon

Du kender sikkert trekantsarealformlen:
$\small \begin{array}{lllllll}&& T=\frac{1}{2}\cdot a\cdot b\cdot \sin(C)\qquad \frac{b}{\sin(B)}=\frac{a}{\sin(A)}\Rightarrow b=a\cdot \frac{\sin(B)}{\sin(A)}\\\\&\textup{hvoraf:} \\&&T=\frac{1}{2}\cdot a\cdot a\cdot \frac{\sin(B)}{\sin(A)}\cdot \sin(C)=\frac{a^2}{2}\cdot \frac{\sin(B)\cdot \sin(C)}{\sin(A)} \end{array}$

Brugbart svar (0)

Svar #10
19. marts 2023 af ringstedLC

b) En n-sidet polygon med siden s:

$\begin{align*} A &= \tfrac{1}{4}n\cdot s^2\cdot \cot\!\left (\frac{\pi}{n}\right )&&,\;\cot(v)=\frac{\cos(v)}{\sin(v)} \end{align*}$

Brugbart svar (0)

Svar #11
19. marts 2023 af ringstedLC

c) Brug ensvinklede trekanter:

$\begin{align*} \frac{20}{13} &= \frac{\frac{L}{2}}{\frac{l}{2}}=\frac{L}{l} \\ L &= 34\cdot \frac{20}{13}\approx ... \end{align*}$

Vedhæftet fil:_0.png

Brugbart svar (0)

Svar #12
19. marts 2023 af ringstedLC

$\begin{align*} \tan\bigl(v-90^{\circ}\bigr) &= \frac{\frac{L\,-\,l}{2}}{H} \end{align*}$

Vedhæftet fil:_0.png

Svar #13
23. marts 2023 af fjg5th

er lidt i tvivl med de formler i b, c og d? nogen der kan fortælle mig og forklare yderligere?

Svar #14
23. marts 2023 af fjg5th

nogen der kan hjælpe mig med opgave b? forstår ikke hvilken formel jeg skal bruge.

Brugbart svar (0)

Svar #15
23. marts 2023 af M2023

#14.

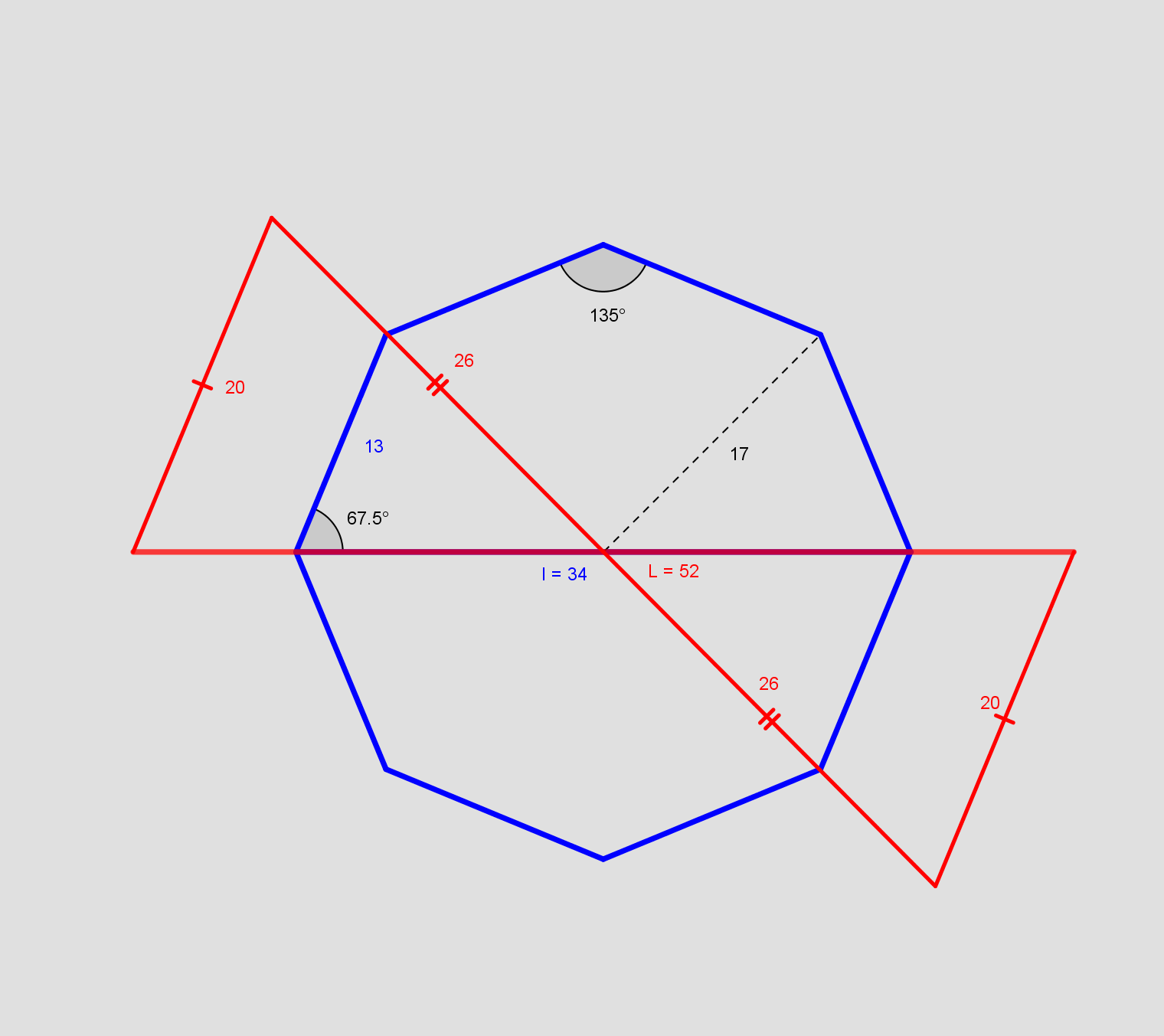
#10...En n-sidet polygon med siden s har arealet, A:
$\begin{align*} A &= \tfrac{1}{4}\cdot n\cdot s^2\cdot \cot\!\left (\frac{\pi}{n}\right )&&,\;\cot(v)=\frac{\cos(v)}{\sin(v)} \end{align*}$

Diameteren, D, i en regulær n-sidet polygon med siden s er

$D=\frac{s}{cos(\frac{\pi }{2}-\frac{\pi}{n}))}$

#12. (Omskrevet)...
$\\ tan \left ( v-\frac{\pi }{2} \right ) = \frac{L\,-\,l}{2\cdot H} \Leftrightarrow$

$v= tan^{-1}\left ( \frac{L-l}{2\cdot H} \right )+\frac{\pi }{2}$

Brugbart svar (0)

Svar #16
23. marts 2023 af ringstedLC

b) Er "bare" en formel, der slås op og anvendes. Den skal ikke forklares.

c) I ensvinklede trekanter er forholdet mellem parvist ensliggende sider det samme.

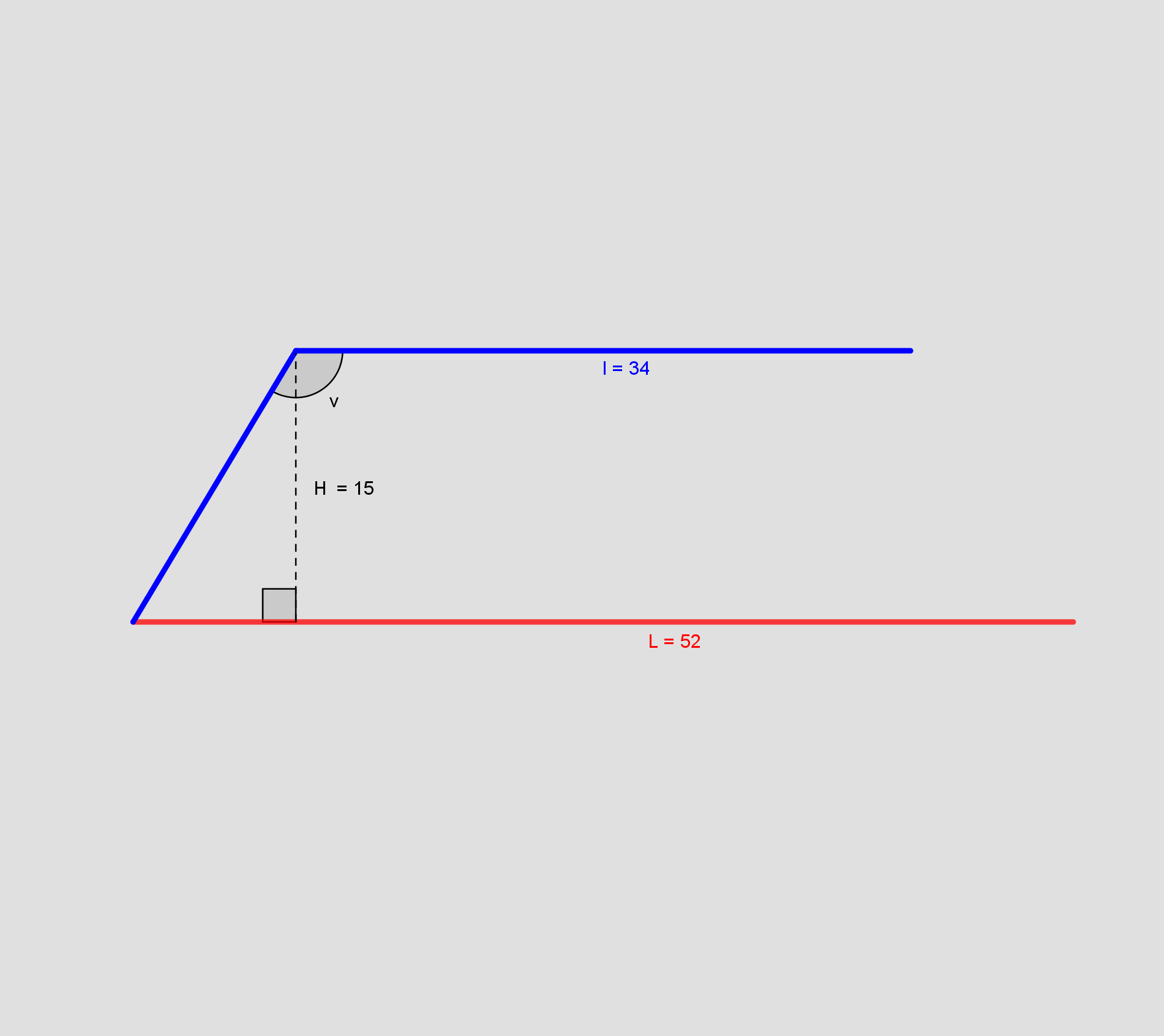
d) Tangens til en vinkel er den modstående- divideret med den hosliggende katete. Bestem v.

Brugbart svar (0)

Svar #17
23. marts 2023 af M2023

#15...c) Diameteren, D, i en regulær n-sidet polygon (hvor n er lige) med siden s er

$D=\frac{s}{cos(\frac{\pi }{2}-\frac{\pi}{n}))}$

Skriv et svar til: hjælp til opgave om volumen

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.