Matematik

Hvordan bestemmer jeg den største tangenthældning for funktionen f?

25. marts 2023 af Okkegokke - Niveau: B-niveau

Vil gerne løse denne opgave med hjælp fra vende tangent.

Men er usikker på hvordan jeg starter

Se vedhæftet fil for at se funktionen

Vedhæftet fil: Capure.PNG

Brugbart svar (0)

Svar #1
25. marts 2023 af ringstedLC

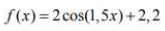
$\begin{align*} \textup{Tangenth\ae ldning}: a=f'(x) &= \bigl(2\cdot\cos(1.5x)+2.2\bigr)' \\ a(x) &= \bigl(2\cdot\cos(1.5x)+2.2\bigr)' \end{align*}$

Bestem nu a_maks som i en monotoniundersøgelse, ved at løse:

$\begin{align*} a'(x)=0 &= \bigl(2\cdot\cos(1.5x)+2.2\bigr)'' \end{align*}$

NB. Husk at trigonometriske funktioner er periodiske og at ligningen derfor har uendelig mange løsninger. For overblik; tegn f ' og f '' fx i intervallet 0 ≤ x ≤ 2π

Svar #2
25. marts 2023 af Okkegokke

Har dog stadig problemer med at forstå hvordan funktionen bliver differentieret ved vende tangent.

Brugbart svar (0)

Svar #3
25. marts 2023 af ringstedLC

#2
Har dog stadig problemer med at forstå hvordan funktionen bliver differentieret ved vende tangent.

Du må have misforstået et eller andet. Kom eventuelt med en tekst el. figur.

Brugbart svar (0)

Svar #4
26. marts 2023 af AMelev

Hvad får du f '(x) til?
Hvilket CAS-værktøj benytter du?

Du kan udnytte, at sin svinger mellem -1 og 1 og har sit max i π/2+p·π, hvor p er et helt tal.

Skriv et svar til: Hvordan bestemmer jeg den største tangenthældning for funktionen f?

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.