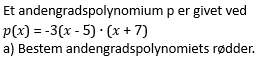Matematik

Rødder i andengradspolynomium

20. november 2023 af blis1204 - Niveau: C-niveau

Hejsa!

Hvordan løser man dette når der er paranteser?

Tak på forhånd:)

Vedhæftet fil: mattt.PNG

Brugbart svar (0)

Svar #1
20. november 2023 af mathon

Brugbart svar (0)

Svar #2
20. november 2023 af mathon

Brug nul-reglen:

Når mindst én af faktorerne i et produkt er lig med nul, er produktet lig med nul.

For hvilket x er (x - 5) lig med nul.

For hvilket x er (x + 7) lig med nul.

(Du har blot andengradspolynomiet på faktoriseret form.)

Brugbart svar (0)

Svar #3
20. november 2023 af mathon

Som kontrol:
find rødderne i andengradspolynomiet -3x²- 6x + 105

Svar #4
20. november 2023 af blis1204

Hmmm, så a er -3, b er x-5 og c er x+7 eller hvordan?

Brugbart svar (0)

Svar #5
20. november 2023 af mathon

så
$\small \begin{array}{lllllll} \begin{matrix} a&=&-3\\b&=&-6 \\c&=&105 \end{matrix} \end{}$

Brugbart svar (0)

Svar #6
20. november 2023 af mathon

$\small \begin{array}{lllllll}&& p(x)=-3\cdot \left ( x-5 \right )\cdot (x+7)\\\\\textup{ved brug af nul-reglen}\\\textup{har du r\o dderne:}\\&&x=\left\{\begin{matrix} -7\\5 \end{matrix}\right. \end{}$

Brugbart svar (0)

Svar #7
20. november 2023 af ringstedLC

Formen for p kaldes faktoriseret fordi den består af faktorerne "-3", "(x - 5)" og "(x +7)".

Rødder ved faktoriseret form:

$\begin{align*}\textup{Nulreglen}:0 &= a\cdot b &\Rightarrow a=0 &\vee b=0 \\ p(x)=0 &= -3\cdot (x-5)\cdot (x+7) \\ 0 &= (x-5)\cdot (x+7) &\Rightarrow x-5=0 &\vee x+7=0 \\ &&\Rightarrow x=...=r_1 &\vee x=...=r_2 \\ \textup{Kontrol}:\\ p\bigl(r_1\bigr)=0 &= -3\cdot \bigl(r_1-5\bigr)\cdot \bigl(r_1+7\bigr) \\ p\bigl(r_2\bigr)=0 &= -3\cdot \bigl(r_2-5\bigr)\cdot \bigl(r_2+7\bigr)\end{align*}$

Brugbart svar (0)

Svar #8
20. november 2023 af ringstedLC

I #3 ses p på standardformen med tre led som fås ved at gange "-3" ind og gange parenteserne med hinanden:

$\begin{align*} p(x) &= -3\cdot (x-5)\cdot (x+7) \\ &= (-3x+15)\cdot (x+7) \\ &= -3x^2-21x+15x+105 \\ p(x) &= -3x^2-6x+105 \\ \textup{R\o dder}:\\ 0 &= -3x^2-6x+105 \\\frac{0}{-3}=0 &= x^2+2x-35=\frac{-3x^2-6x+105}{-3} \\ x &= \frac{-2\pm\sqrt{2^2-4\cdot 1\cdot (-35)}}{2\cdot 1} \\ x &= \left\{\begin{matrix}r_1=...\\r_2=...\end{matrix}\right. \end{align*}$

Svar #9
20. november 2023 af blis1204

Jeg må ikke bruge redskaber til dette så får ikke mit resultat til -7 og 5, men til -kvadratrod af 34+1 og kvadratrod af 34-1

Er det stadig rigtigt?

Brugbart svar (0)

Svar #10
20. november 2023 af Anders521

#9 Nej.

Brugbart svar (0)

Svar #11
20. november 2023 af ringstedLC

#9
Er det stadig rigtigt?

Nej. Løsningerne er som i #5. Fejlen ligger ofte i diskriminanten:

$\begin{align*} 5=\frac{-2\,{\color{Red} +}\,\sqrt{d}}{2} &= -\frac{2}{2}+\frac{\sqrt{d}}{2} \\ &= \frac{\sqrt{d}}{2}-1\;{\color{Red} \neq }\;\sqrt{d}-1 \\ 5+1 &= \frac{\sqrt{d}}{2} \\\sqrt{d} &= 2\cdot (5+1) \\ d &= \bigl(2\cdot (5+1)\bigr)^{2}=144 \end{align*}$

Prøv så at finde regnefejlen(ene) i din diskriminant!

Brugbart svar (0)

Svar #12
21. november 2023 af mathon

$\small \begin{array}{lllllll} \sqrt{d}=&\sqrt{(-6)^2-4\cdot \left ( -3 \right )\cdot 105}=\\\\& \sqrt{36+12\cdot 105}=\\\\& \sqrt{36+12\cdot 7\cdot 3\cdot 5}=\\\\& \sqrt{36+(12\cdot 3)\cdot 35}=\\\\& \sqrt{36+36\cdot 35}=\\\\& \sqrt{36\cdot \left ( 1+35 \right )}=\\\\& \sqrt{36^2}=\\\\&36\\\\\\ -3x^2-6x+105=0\\\\& x=\frac{-(-6)\pm\sqrt{d}}{2\cdot (-3)}=\frac{6\pm36}{-6}=-1\mp6=\left\{\begin{matrix} -7\\5 \end{matrix}\right. \end{}$

Brugbart svar (0)

Svar #13
21. november 2023 af mathon

eller ved division med -3:

$\small \begin{array}{lllllll} -3x^2-6x+105=0\\\\&& x^2+2x-35=0\\\\\\& \sqrt{d}=&\sqrt{2^2-4\cdot 1\cdot \left ( -35 \right )}=\\\\&&\sqrt{2^2\cdot \left ( 1+35 \right )}=\\\\&&\sqrt{2^2\cdot 6^2}=\\\\&& 2\cdot 6=\\\\&&12\\\\\\ x^2+2x-35=0\\&& x=\frac{-2\mp\sqrt{d}}{2\cdot 1}=\frac{-2\mp12}{2}=-1\mp6=\left\{\begin{matrix} -7\\5 \end{matrix}\right. \end{}$

Brugbart svar (0)

Svar #14
21. november 2023 af mathon

#0
   ALT dette kunne du være "sluppet for",
   hvis du havde benyttet/kendt nul-reglen,
   som i #6 eller #7.

Skriv et svar til: Rødder i andengradspolynomium

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.