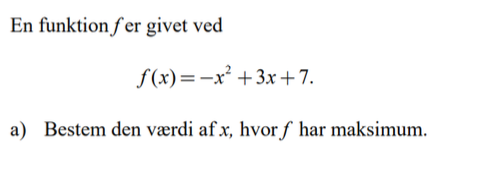Opgave

f ' (x) = 0 løses for at bestemme maksimum.

Du bestemmer f'(x) = 0 for at finde alle ekstrema (dvs. både minimum og maksimum, hvis funktionen har begge). Opgaven fortæller dig, i dette tilfælde, at du skal finde maksimum, og du ved derfor at alle x-værdier, som opfylder f'(x) = 0 må være når funktion f har maksimum.

Kan det godt passe, at svaret er 0,66?... 

Nej. Det er hurtigt at tjekke ved at tegne grafen for f

#0 Det er ikke tilstrækkeligt at at bestemme f '(x) = 0. Der skal et argument til at der netop er tale om et maksimum (og ikke et minimum).

Alternativ kan man bruge sin viden om andengradspolynomier ang. den ledende koefficients fortegn. og dermed beregne x-koordinaten til toppunktet.

Kan jeg ikke bar skrive sådan her?

0 = -2x+3

-3-0= -2x

-3-/-2= 1.5

Maks er 1.5?

#7 Ja, x = 1,5 er løsningen til ligningen f '(x) = 0.

#6

#0 Det er ikke tilstrækkeligt at at bestemme f '(x) = 0. Der skal et argument til at der netop er tale om et maksimum (og ikke et minimum).

Alternativ kan man bruge sin viden om andengradspolynomier ang. den ledende koefficients fortegn. og dermed beregne x-koordinaten til toppunktet.

Har du evt. mulighed for at uddybe, hvorfor beregningen ikke er tilstrækkelig? I denne opgave er det i forvejen blevet givet, at der er tale om et maksimum - eller mener du for elevens egen forståelse?

Jeg er dog enig med den resterende del af besvarelsen.