Matematik

Beregn længden

15. oktober 2013 af ITChem (Slettet) - Niveau: B-niveau

Hej!

Er der nogen som kan hjælpe mig med dette spørgsmål:

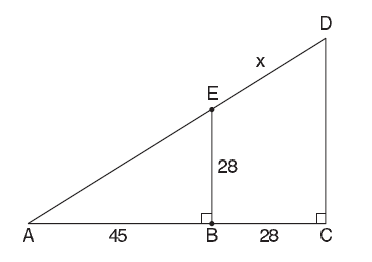
Beregn længden af det med x mærkede stykke med 2 decimaler.

I kan se figuren i den vedhæftet fil på side 51.

Tak på forhånd

Vedhæftet fil: matA1opgaver.pdf

Brugbart svar (0)

Svar #1
15. oktober 2013 af mathon

Beregn |AE|.

Benyt ensvinklede trekanter.

Svar #2
15. oktober 2013 af ITChem (Slettet)

ahhh, tak for det :D

Svar #3
15. oktober 2013 af ITChem (Slettet)

du må undskylde men har mistet forståelsen igen, men hvordan skal jeg beregne AE?

Brugbart svar (2)

Svar #4
15. oktober 2013 af mathon

…hypotenusen i en retvinklet trekant.

Brugbart svar (0)

Svar #5
15. oktober 2013 af Andersen11 (Slettet)

Du skal afholde dig fra at publicere copyrighted materiale på internettet, som du ikke har ophavsretten til.

Brugbart svar (0)

Svar #6
15. oktober 2013 af lvr34 (Slettet)

Bestem hypotenusen i den retvinklede trekant AEB, altså længden AE. Udled derefter proportionalitetsfaktoren imellelem AEB og ADC og benyt da denne til at bestemme længden af hypotenusen i trekanten ADC, altså længden AD. Derefter trækkes længden AE fra længden AD og dermed haves værdien for det markerede stykke, X.

Brugbart svar (0)

Svar #7
15. oktober 2013 af Andersen11 (Slettet)

Man har

Vedhæftet fil:Trekant.png

Svar #8
17. oktober 2013 af ITChem (Slettet)

Tusind tak for svarene! :D

Brugbart svar (0)

Svar #9
21. november 2013 af denise94 (Slettet)

Jeg sidder med den samme opgave som denne, og super god forklaring!

Men hvordan finder jeg frem til proportionalitetsfaktoren ??? :-)

Brugbart svar (0)

Svar #10
21. november 2013 af Andersen11 (Slettet)

Benyt, at trekant ABE er ensvinklet med trekant ACD. Man kender længderne af de ensliggende sider AB og AC.

Brugbart svar (0)

Svar #11
06. maj 2021 af Skoledum

står med samme opgave hvad var svaret ?

Brugbart svar (0)

Svar #12
08. maj 2021 af mathon

$\begin{array}{lllll}&& \Delta ABE\sim\Delta ACD\\\\&& \frac{\left | AB \right |}{\left | AC \right |}=\frac{\left | AE \right |}{\left | AE \right |+x}\\\\&& \frac{\left | AC \right |}{\left | AB \right |}=\frac{\left | AE \right |+x}{\left | AE \right |}\\\\&& \frac{\left | AC \right |-\left | AB \right |}{\left | AB \right |}=\frac{\left | AE \right |+x-\left | AE \right |}{\left | AE \right |}\\\\&& \frac{28}{45}=\frac{x}{53}\\\\&& x=\frac{28}{45}\cdot 53 \end{array}$

Brugbart svar (0)

Svar #13
09. maj 2021 af mathon

Den der husker, at en paralleltransversal deler trekantsiderne i proportionale stykker,
kommer lidt hurigere til sammenhængen:

$\begin{array}{lllll}&& \frac{x}{53}=\frac{28}{45}\\\\&& x=\frac{28}{45}\cdot 53 \end{array}$

Skriv et svar til: Beregn længden

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.