Matematik

Udledning af en formel

21. november 2015 af Rina68 - Niveau: Universitet/Videregående

Hejsa,
Jeg er gået lidt i stå med en udledning og håber på at nogen kan hjælpe.
Jeg skal vise at ?” F(J) kan blive udtrykt som: V_R(J-1)-V-P(J-1) =4B_0 - 6D_j)((J+½)-8D_J(J+½)^3
Se vedhæftede.
Jeg er kommet en del igennem, men kan ikke lige gennemskue den sidste del.

Vedhæftet fil: Q2.docx

Brugbart svar (0)

Svar #1
21. november 2015 af Therk

Ligning 2 i det røde har vist, på højre side, et led for meget og potenserne er 1 for høje. Den ligning gælder i hvert fald kun for J = -1 og J = 0 på sin nuværende form.

Hvad mener du med symbolet

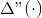
Kan du evt. uploade eqn. 13?

Ligningen under "This can be re-written into:": Er det en Δ"F(J)-ligning? Ellers kan jeg ikke se hvordan du er kommet frem til den reducering. Og ligningen lige over: Skal det være F i stedet for E?

Svar #2
21. november 2015 af Rina68

Hele opgaven er oploaded. Spørgsmålet står på sidste side og på side 6 stå eq 13.
Ja, det er en en Δ"F(J)-ligning ligning.
Og jeg vil mene at der skal stå E?
Hvad mener du med med lighning 2 i det røde? Jeg er ikke sikker på hvor fejlen er?

Vedhæftet fil:26130_The Vibrational-Rotational Spectrum and Molecular Equilibrium Structure of Carbon Dioxide.pdf

Brugbart svar (1)

Svar #3
21. november 2015 af Therk

I dokuementet i #0 er der, i bunden, en fejl i det, du har skrevet med rødt:

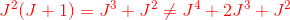
$\color{red}J^2(J+1) = J^3+J^2 \neq J^4+2J^3 + J^2$

medmindre J = 0 eller J = -1.

$\rule{7cm}{0.4pt}$

Jeg er nu næsten sikker på at der skal stå F, medmindre jeg fuldstændig misforstår det du laver.

Du bruger at

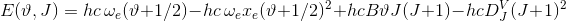
$E(\vartheta, J ) = hc\,\omega_e(\vartheta+1/2) - hc\, \omega_ex_e(\vartheta+1/2)^2 + hcB\vartheta J(J+1) - hcD_J^V(J+1) ^2$

så hvis vi dividerer med hc på begge sider får vi

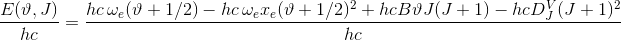
$\frac{E(\vartheta,J)}{hc} = \frac{hc\,\omega_e(\vartheta+1/2) - hc\, \omega_ex_e(\vartheta+1/2)^2 + hcB\vartheta J(J+1) - hcD_J^V(J+1) ^2}{hc}$

og så bruger du at

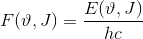
$F(\vartheta,J) = \frac{E(\vartheta,J)}{hc}$

så

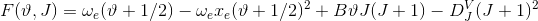
$F(\vartheta,J) = \omega_e(\vartheta+1/2)-\omega_ex_e(\vartheta+1/2)^2+B\vartheta J(J+1)-D_J^V(J+1)^2$

se fx eqn. (15).

$\rule{7cm}{0.4pt}$

Dernæst bruger du at

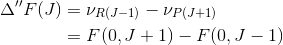
$\begin{align*} \Delta''F(J) &= \nu_{R(J-1)} - \nu_{P(J+1)}\\ & = F(0,J+1) - F(0,J-1) \end{align*}$

og indsætter rigtigt nok for vartheta = 0 og så er der en masse, som går ud med hinanden. Så er det bare at gå amok med algebraen.

Det sidste du har:

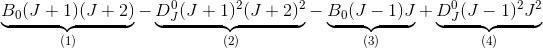
$\underbrace{B_0(J+1)(J+2)}_{(1)} -\underbrace{D_J^0(J+1)^2(J+2)^2}_{(2)}-\underbrace{B_0(J-1)J}_{(3)}+\underbrace{D_J^0(J-1)^2J^2}_{(4)}$

giver os:

$\begin{align*} (1) &= {\color{red}B_0 J^2} +3B_0J+2B_0\\ (2) &= D_J^0({\color{red}J^4}+6J^3+13J^2+12J + 4) \\ (3) &= {\color{red}B_0 J^2}- B_0J \\ (4) &= D_J^0 (J^2+1-2J)J^2 = D_J^0 ({\color{red}J^4}+J^2-2J^3) \end{align*}$

Det med rød går umiddelbart ud med hinanden, se fortegnene på (1), (2), (3) og (4).

Hvis du herfra bare ganger ud og reducerer, står du på et tidspunkt tilbage med led med D_J⁰ tilsvarende højre side af eqn. (20). og så kan du bare bruge den givne relation! Læg derudover mærke til at

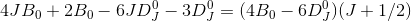
4JB_0 +2B_0 - 6JD_J^0 -3D_J^0 = (4B_0-6D_J^0)(J+1/2)

og det skulle gerne være dine resterende led - dermed er du færdig! Hvis du ikke umiddelbart kan overbevise dig om at det sidste herover er sandt, så se at

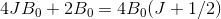
4JB_0 +2B_0= 4B_0(J+1/2)

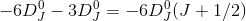
-6D_J^0 -3D_J^0 = -6D_J^0(J+1/2)

De har (J+1/2) tilfældes, så træk det ud for parentes. Og så er du færdig.

Svar #4
22. november 2015 af Rina68

tak:)

Det giver mening

Skriv et svar til: Udledning af en formel

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.