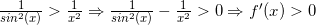Matematik
Vis funktion er strengt voksende
Se vedhhæftet fil.
Har løst den første delopgave, men ved ikke, hvordan jeg skal gribe den anden delopgave an.
Jeg tænker at jeg kan vise at:
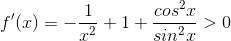
Er det her, at jeg skal bruge den nævnte ulighed i opgavebeskrivelsen? I så fald er jeg i tvivl om, hvordan den benyttes konkret.
Mvh.
Svar #2
29. juni 2017 af peter lind
-1/x2 + 1+cos2(x)/sin2(x) = -1/x2 + (sin2(x)+cos2(x))/sin2(x) = -1/x2+1/sin2(x) >0 <=> -sin2(x)+x2> 0
Svar #3
29. juni 2017 af Soeffi
#0. Du har, at
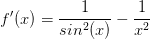
Da sin2(x) = |sin(x)|2 gælder, at sin2(x) < x2. Dermed er 1/sin2(x) > 1/x2 og dermed er f'(x) > 0.
Svar #4
29. juni 2017 af JohnDoe1990
Ahh... Okay. Så tricket her var for mig at:
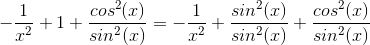
Mange tak. Det giver god mening. :-)
Skriv et svar til: Vis funktion er strengt voksende
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.








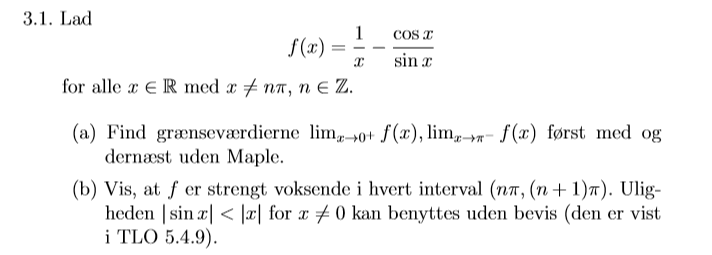
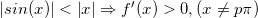 . Du har:
. Du har: