Inertimoment omkring forskudt akse ift.massemidtpunkt

Regn inertiomentet ud for kuglen i a I_a. Inertimomentet omkring b er så I_a+m*L². Adder derefter inertimomentet fra kuglen i b.

#1

Regn inertiomentet ud for kuglen i a I_a. Inertimomentet omkring b er så I_a+m*L². Adder derefter inertimomentet fra kuglen i b.

Har den masseløse stang ingen indflydelse?

nej ikke når den er masseløs

#3

nej ikke når den er masseløs

Okay. Skal jeg så forstå det du skriver i #1 som?

Hvor 

nej.  D har misforstået det. Inertimomentet fra kuglen i a omkring b er I_a+m_a*L². Til det skal du addere inertimomentet fra kuglen i b

#5

nej.  D har misforstået det. Inertimomentet fra kuglen i a omkring b er I_a+m_a*L². Til det skal du addere inertimomentet fra kuglen i b

Aah okay forstår det nu. Mange tak. Kan man ikke også finde inertimomentet omkring massemidtpunktet (selvom stangen er masseløs)? Det jeg oprindeligt gjorde var at finde ud af, hvor langt der var fra massemidtpunktet (som lå på stangen) hen til hhv. masse a og b.

 Jo men det bliver mere kompliceret. Du skal først beregne inertimonenterne for kuglerne. Derefter skal du paralelforskyde, hver af kuglerne til massemidtpunkterne og addere inertimomenterne. Til slut skal du parallelforskyde inertimomentet til b

Trådstarter efterlyser, hvordan man finder inertimomentet om en akse, der ikke går gennem massemidtpunktet, når man kender indertimomentet om massemidtpunktet.

Inertimomentet om a-aksen er I_a = I_T + (m_a + m_b)*L_a², hvor L_a er a-aksens afstand fra massemidtpunktet.

Jeg har regnet I_T ud til 114kgm², hvilket ikke stemmer med dit resultat. Hvordan har du regnet det ud?

Tådstarteren starter med at skive "Jeg er i gang med at regne inertimomentet omkring aksen b på ovenstående tegning." og det er det jeg reagerede på. Jeg har ikke direkte regnet noget ud; men oplyst hvordan man regner inertimomentet ud omkring b. I #7 har jeg angivet (som et mellemresultat) en metode til at regne tyngdepuktet ud for massemidtpunktet. Er det den du hentyder til? Hvordan er du kommet frem til I_T?

Jeg startede med at udregne inertimomentet omkring massemidtpunktet, som ligger på stangen. Her fik jeg inertimomentet 36 kg*m^2.  Nu vil jeg gerne beregne inertimomentet omkring aksen b, vha. parallel-akse teoremet, men jeg er usikker på hvilken afstand og masse jeg skal indsætte. Kan i mon hjælpe her?

Det er dette, jeg er gået ud fra. Det er sidste del af #0.

Jeg ved ikke, hvordan trådstarter har regnet I_T ud, men jeg kommer til et andet resultat. Min metode:

Jer har regnet inertimomenterne af kuglerne ud (om deres respektive centre). Dernæst har jeg regnet inertimomenterne og massemidtpunktet ud ved hjælp af udtrykket for forskudt akse: I_aT = I_a + m_a*L_a² og tilsvarende for b.

Din metode er helt afgjort den enkleste og den, jeg selv ville vælge, men når trådstarter har regnet inertimomentet om massemidtpunktet ud og gerne vil videre der fra, vil jeg gerne prøve at følge op på det. Desuden har jeg mistanke om, at trådstarter har regnet forkert, så jeg vil gerne se beregningerne.

Det skal bemærkes, at #7 kom mens jeg var ved at skrive #8.

Jeg har højst sandsynligt regnet det forkert, men lad mig forklare min tankegang vha. en tegning.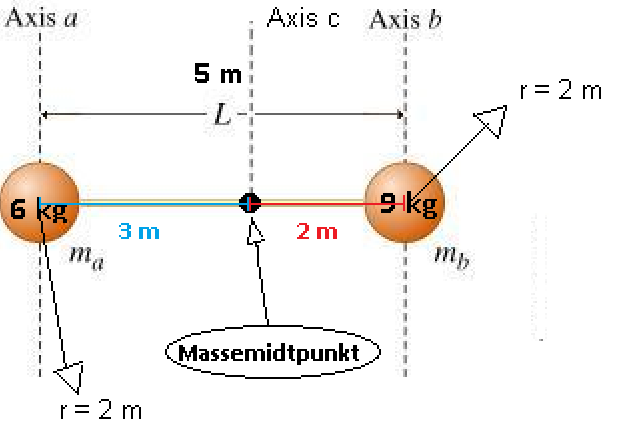

Foroven ses det scenarie som jeg tænkte mig. Jeg startede med at udregne massemidtpunktets placering med udgangspunkt i centrum af massen . Derved fik jeg massemidtpunktet til at være 3 meter til højre fra centrum af massen a. Jeg regner forresten med at stangen går fra centrum til centrum af kuglerne (dette er muligvis forkert).Nu ville jeg så regne inertimomentet omkring massemidtpunktet (axis c/akse c). Det regnede jeg så på følgende måde: . Fortæl meget gerne, hvor den går galt henne.

Inertimomentet af en kugle om dens centrum er 2/5 m*r². Her skal du altså bruge de 2m, der er kuglens radius.

Inertimomentet af en punktformig masse, m, om et punkt, P, i afstanden s fra massen er m*s². Det samlede inertimoment for en kugle om P er summen af kuglens inertimoment om dens centrum og inertimomentet af en punktformig masse på kuglens sted om P: I = 2/5 m*r² + m*s². Du har blandet de to udtryk sammen.

Dette er faktisk et tilfælde af den regel, du efterspørger i sidste del af #0. Det er også den, som er brugt i #1, hvor problemet angribes ved direkte at vælge b-aksen.

#12

Inertimomentet af en kugle om dens centrum er 2/5 m*r². Her skal du altså bruge de 2m, der er kuglens radius.

Inertimomentet af en punktformig masse, m, om et punkt, P, i afstanden s fra massen er m*s². Det samlede inertimoment for en kugle om P er summen af kuglens inertimoment om dens centrum og inertimomentet af en punktformig masse på kuglens sted om P: I = 2/5 m*r² + m*s². Du har blandet de to udtryk sammen.

Dette er faktisk et tilfælde af den regel, du efterspørger i sidste del af #0. Det er også den, som er brugt i #1, hvor problemet angribes ved direkte at vælge b-aksen.

Er det så ikke muligt at vælge c-aksen, som går gennem massemidtpunktet, og beregne inertimomentet om b-aksen ud fra inertimomentet om c-aksen?

Jo se #7

#14

Jo se #7

Okay. Ja det var noget af en omvej, så foretrækker helt klart din metode. To spørgsmål: 1) Kan man altid lave denne betragtning, så længe det objekt, der forbinder kuglerne er masseløs? 2) Hvis stangen nu havde en masse, hvad ville man så skulle gøre?

Ja.

Hvis stangen havde en masse skulle man addere stangens inertimoment m_s*L²/3