Matematik

Bestem ligning for aplha - funktioner af to variable

16. april 2019 af caro96 - Niveau: A-niveau

Jeg har lidt svært ved at gennemskue hvad jeg skal i denne opgave i B, er der nogen der kan hjælpe? :-)

Vedhæftet fil: 57079826_2340530099553643_4039317747186794496_n.jpg

Brugbart svar (0)

Svar #1
16. april 2019 af StoreNord

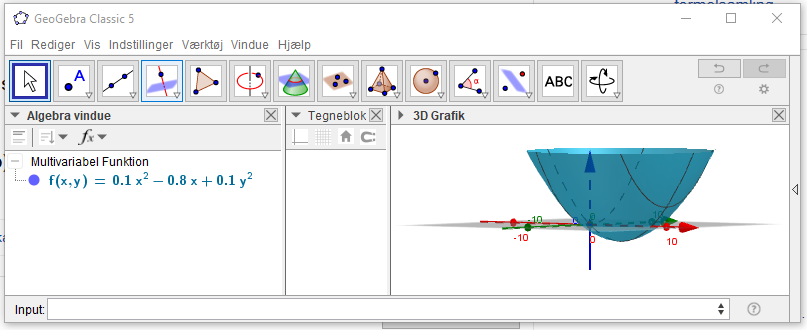
b) Hvis du har tegnet den i 3D, for eksempel i Geogebra, kan du se , at α er xy-planet.

Brugbart svar (0)

Svar #2
16. april 2019 af StoreNord

c) For cirklen gælder: a(x, y) = 0.1x² - 0.8x + 0.1y² = 0.9

Kan du genkende cirklens ligning?

Brugbart svar (0)

Svar #3
16. april 2019 af StoreNord

RETTELSE:
# 1 er noget værre vrøvl. Minimum er under xy-planet.

Men #2 om cirklen er rigtigt!

Svar #4
16. april 2019 af caro96

Jeg har brugt maple til at tegne grafen, og den ser ud som på billedet. Jeg kan ikke se hvordan mit minimum kan hjælpe til at bestemme α?

Ift dit svar i c, lyder cirklens ligning (x-a)^2+(y-b)^2=r^2, hvordan kan får du det til : a(x, y) = 0.1x² - 0.8x + 0.1y² = 0.9?

Vedhæftet fil:Skærmbillede 2019-04-16 kl. 23.34.04.png

Brugbart svar (0)

Svar #5
17. april 2019 af Capion1

c) Man har:
0,1x² - 0,8x + 0,1y² = 0,9
Gang igennem med 10:
x² - 8x + y² = 9
(x - 4)² - 16 + y² = 9
(x - 4)² + (y - 0)² = 5²
Hvad ser vi da?

Brugbart svar (0)

Svar #6
17. april 2019 af StoreNord

For at finde x- og y for minimum skal du aflede funktionen med hensyn til x henholdsvis y og sætte dem lig med 0.
Så indsætter de fundne x- og y-værdier i funktoonen, og finder z-værdien.

Vedhæftet fil:Udklip22.PNG

Brugbart svar (0)

Svar #7
17. april 2019 af ringstedLC

#6: Jeg opfatter opgaveteksten som at "stangen" er monteret vinkelret på skærmen i P.

$\begin{align*} f(x,y) &= 0.1x^2-0.8x+y^2 \\ f(x) &= 0.1x^2-0.8x\;,\;y=P_y=0\Downarrow \\ f'(x) &= 0.2x-0.8\Downarrow \\ f'(x) &= -0.8\;,\;x=P_x=0 \end{align*}$

Linje i α med y = 0:

$\begin{align*} \begin{pmatrix}x\\z\end{pmatrix} &= \begin{pmatrix}0\\0\end{pmatrix}+ t\cdot \begin{pmatrix}1\\-0.8\end{pmatrix}\Downarrow \\ \overrightarrow{n_{\alpha}} &= \widehat{\begin{pmatrix}1\\-0.8\end{pmatrix}}= \begin{pmatrix}0.8\\1\end{pmatrix}\Downarrow \\ \text{Planen }\alpha &: 0.8x+z=0 \end{align*}$

Vedhæftet fil:A_M_071 - Lampeskærm_caro96.png

Brugbart svar (0)

Svar #8
17. april 2019 af StoreNord

Ja. Du har ret. Så blev den godt nok lidt sværere!

Svar #9
19. april 2019 af caro96

#5 - Jeg kan ikke lige gennemskue hvor du får a=4 og b=0 fra? Samt r^2=5^"? Så vidt jeg lige kan se er det vel cirklens ligning (x-a)^2+(y-b)^2=r^2 du benytter?

#7 - Er det rigitg forstået hvis du differenciere i forhold til x, og derved får y=0? Og hvordan får du f'(x) til at være -0.8? når jeg diffinere den i maple bliver der 0.2

Vedhæftet fil:Skærmbillede 2019-04-19 kl. 09.53.36.png

Brugbart svar (0)

Svar #10
19. april 2019 af ringstedLC

#9: I #5 har du cirklens ligning på en anden form end "centrum-radiusformen". Ved at kvadratkomplementere fås den ønskede form.

#7?: Nej. Når der står:

$\begin{align*} f(x) &= 0.1x^2-0.8x\;,\;y=P_y=0 \\ \text{betyder det}: f(x,0) &= 0.1x^2-0.8x \\ \text{{\color{Red} og ikke}}: \: \: \: \: f(x) &= y=0 \end{align*}$

Der er for det første ikke differentieret noget og efter kommaet står en betingelse for f, ikke et resultat. Jeg laver en "1D funktion" eller et snit gennem skærmen i xz-planen. Den differentieres for at bestemme hældningen af α i P:

$\begin{align*} f'(x) &= 0.2x-0.8 \\ \text{Igen udtrykket}: \: f'(x) &= -0.8\;,\;x=P_x=0 \\ \text{betyder}: \: f'(0) &= -0.8 \\ \text{{\color{Red} og ikke}}: f''(x) &= 0.2 \end{align*}$

Skriv et svar til: Bestem ligning for aplha - funktioner af to variable

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.