Matematik

Analytisk plangeometri - find punkterne for A, B & C

25. maj 2019 af me002 - Niveau: B-niveau

Hej.

Jeg har lidt svært med at forstå denne opgave fordi, når jeg sætter ligningerne ind i geogebra, så bliver der ikke konstrueret en trekant. Jeg har haft isoleret y i alle lignineren, men det hjælper ikke. Håber evt, i kan foreklar mig, hvad jeg gør forkert.

Vedhæftet fil: opgave_230.PNG

Brugbart svar (0)

Svar #1
25. maj 2019 af peter lind

Brugbart svar (1)

Svar #2
25. maj 2019 af peter lind

Du skal se på ligningerne for AB og BC. De har et fælles punkt nemlig B, så koordinaterne for B opfylder begge ligninger. Så løs ligningssystemet 2x+y=11∧2x-y=17. Løsningen er koordinaterne til B.

På tilsvarende måde finder du koordinaterne til A og C

Brugbart svar (0)

Svar #3
26. maj 2019 af mathon

$\small \begin{array}{lllll} \textup{sk\ae ringspunkt B:}\\ &4x=28\\ &x=7&\textup{indsat i }2x+y=11\\ &2\cdot 7+y=11\\ &y=-3\\ &B=(7,-3)\\\\ \textup{sk\ae ringspunkt A:}\\ &-4x-2y=-22\\ &\underline{\, \, \, \, \, \, \, \, x+2y=\, \, \, \, 16}\\ \textup{addition:}&-3x=-6\\ &x=2&\textup{indsat i }2x+y=11\\ &2\cdot 2+y=11\\ &y=7\\ &A=(2,7)\\\\ \textup{sk\ae ringspunkt C:}\\ &4x-2y=34\\ &\underline{\, \, \, x+2y=16}\\ \textup{addition:}&5x=50\\ &x=10&\textup{indsat i }x+2y=16\\ &10+2y=16\\ &5+y=8\\ &y=3\\ &C=(10,3) \end{array}$

Brugbart svar (0)

Svar #4
26. maj 2019 af mathon

$\small \small \small \begin{array}{lllll} \textup{vinkel C:}\\ \textup{for }a\textup{'s og }b\textup{'s}\\ \textup{normalvektorer}\\ \textup{haves:}&\begin{pmatrix} 2\\-1 \end{pmatrix}\cdot \begin{pmatrix} 1\\2 \end{pmatrix}=2\cdot 1+(-1)\cdot 2=0\\\\ \textup{hvorfor:}&\angle C=90\degree\\\\ \textup{vinkel } A\textup{ og }B\textup{ er derfor \textbf{spidse}.} \end{array}$

Brugbart svar (0)

Svar #5
26. maj 2019 af mathon

$\small \small \begin{array}{lllll} \textup{vinkel A:}&\cos^{-1}\left (\frac{\left |\begin{pmatrix} 2\\1 \end{pmatrix}\cdot \begin{pmatrix} 1\\2 \end{pmatrix} \right|}{\sqrt{2^2+1}\cdot \sqrt{1+2^2}} \right )=\cos^{-1}\left ( \frac{4}{5} \right )=\cos^{-1}(0.8)=36.9\degree\\\\ \textup{vinkel B:}&\cos^{-1}\left (\frac{\left |\begin{pmatrix} 2\\1 \end{pmatrix}\cdot \begin{pmatrix} 2\\-1 \end{pmatrix} \right|}{\sqrt{2^2+1}\cdot \sqrt{2^2+(-1)^2}} \right )=\cos^{-1}\left ( \frac{3}{5} \right )=\cos^{-1}(0.6)=53.1\degree \end{array}$

Brugbart svar (0)

Svar #6
26. maj 2019 af mathon

Brugbart svar (1)

Svar #7
26. maj 2019 af mathon

Brugbart svar (1)

Svar #8
26. maj 2019 af mathon

Mængden af punkter på $\small v_A$ har samme afstand til $\small \angle A\textup{'s}$ vinkelben
og ligger i forhold til
$\small \small \begin{array}{lll} &x+2y-16=0&\textup{i den negative halvplan}\\ &2x+y-11=0&\textup{i den positive halvplan}\\\\ \end{array}$

.
$\small \small \begin{array}{lllll} \textup{hvoraf:}&v_A\textup{:}& -\frac{x+2y-16}{\sqrt{5}}&=&\frac{2x+y-11}{\sqrt{5}}\\\\ && -x-2y+16&=&2x+y-11\\ &&3y=-3x+27 \\\\ &v_A\textup{:}&y=-x+9 \end{array}$

Brugbart svar (1)

Svar #9
26. maj 2019 af mathon

$\begin{array}{llll} m_a\textup{ indeholder}\\ \textup{punkterne} &(2,7)\textup{ og }\left (\frac{10+7}{2},\frac{-3+3}{2} \right )=(8.5,0)\\\\ \textup{hvoraf:}\\\\ &\begin{array}{|c|c|c|c|c|c|c|} x_1&y_1&x_2&y_2&a=\frac{y_2-y_1}{x_2-x_1}&b=y_1-a\cdot x_1&y=ax+b\\ \hline 2&7&8.5&0&a=\frac{0-7}{8.5-2}=-\frac{14}{13}&b=7-\left ( -\frac{14}{13} \right )\cdot 2=\frac{119}{13}&y=-\frac{14}{13}x+\frac{119}{13} \end{array}\\\\ \textup{en ligning for }m_a\textup{:}&m_a\quad 14x+13y=119 \end{array}$

Brugbart svar (1)

Svar #10
26. maj 2019 af mathon

$\small \small \begin{array}{llll} h_a\textup{ er et stykke}\\ \textup{af linjen }&\, \, \, \, \, \, \, \, \, \, \, \, \, 2x+y-11=0\\\\ \textup{hvorfor h\o jden }\\ \textup{har samme ligning:}&h_a\textup{:}\quad2x+y-11=0 \end{array}$

Brugbart svar (0)

Svar #11
26. maj 2019 af mathon

se bort fra #6, som er en fejltastet gentagelse af #5.

Svar #12
26. maj 2019 af me002

Med hensyn til svar #8, hvad betyder negativ og positiv halvplan, og hvorfor tager du kvadratroden af 5.

Brugbart svar (1)

Svar #13
26. maj 2019 af ringstedLC

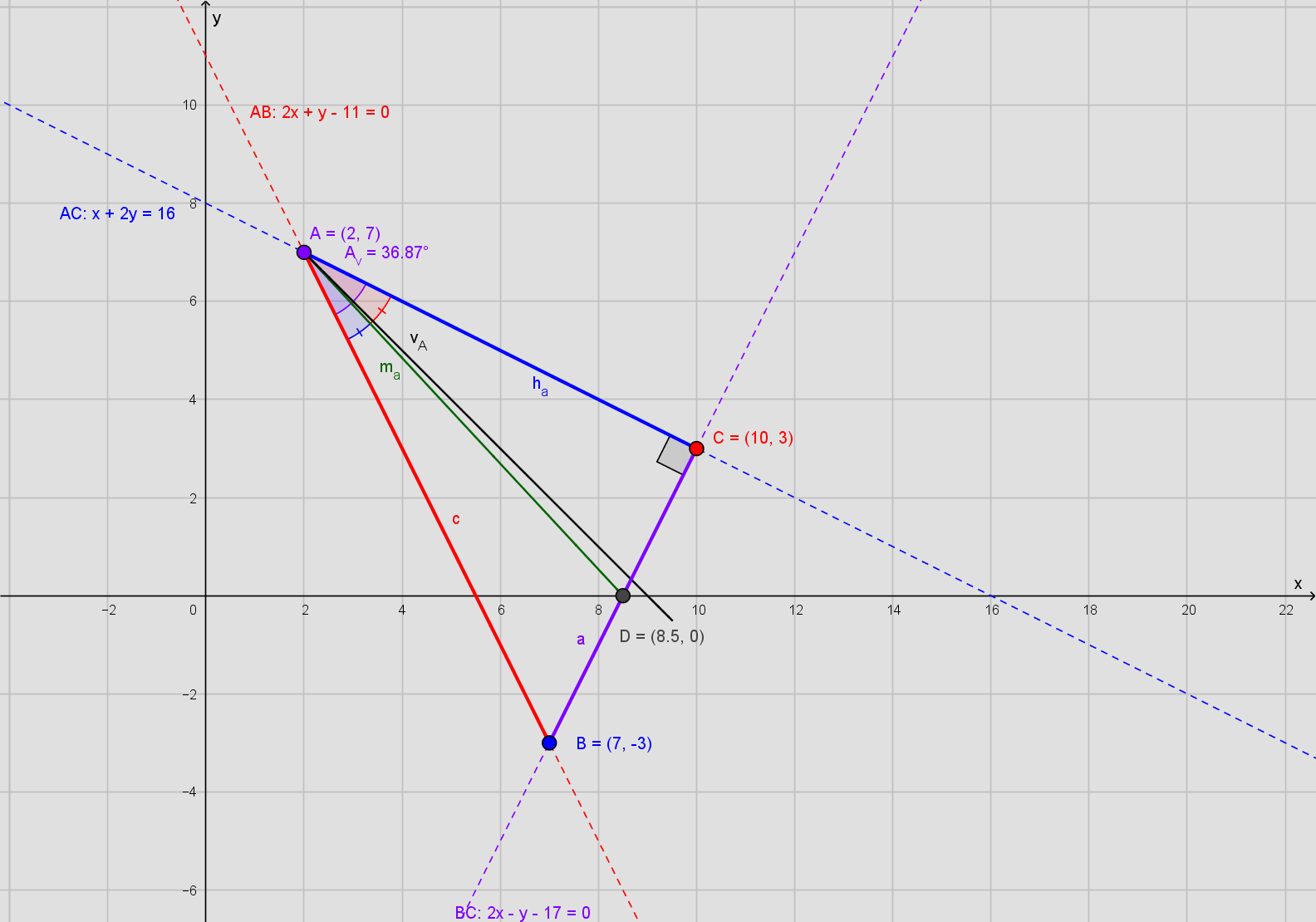
a) Med GeoGebra CAS:

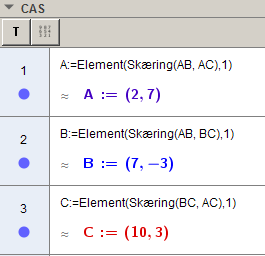
eller:

$\begin{align*} AB:2x+y=11& \\ BC:2x-y=17&\Leftrightarrow y=2x-17 \\ \text{---------------}& \\ 4x=28&\Leftrightarrow x=7\Rightarrow y=2\cdot 7-17=-3 \\ B&:(7,-3) \\ AB:2x+y=11&\Leftrightarrow y=-2x+11 \\ AC:x+2y=16&\Leftrightarrow x+2\cdot \left (-2x+11\right )=16 \\ -3x+22=16&\Leftrightarrow x=2\Rightarrow y=-2\cdot 2+11=7 \\ A&:(2,7) \\ BC:2x-y=17&\Leftrightarrow y=2x-17 \\ AC:x+2y=16&\Leftrightarrow x+2\cdot \left (2x-17\right )=16 \\ 5x-34=16&\Leftrightarrow x=10\Rightarrow y=2\cdot 10-17= 3 \\ C&:(10,3) \\ \end{align*}$

b) Vinkler:

$\begin{align*} AB:2x+y &= 11\Leftrightarrow y=-2x+11 \\ BC:2x-y &= 17\Leftrightarrow y=2x-17 \\ AC:x+2y &= 16\Leftrightarrow y=-0.5x+8 \\ a_{BC}\cdot a_{AC} &= -1\Leftrightarrow BC\perp AC \Leftrightarrow \angle C=90^{\circ} \\ \angle A &= \sin^{-1}\left ( \tfrac{a}{c} \right )=\:?\;^{\circ} \\ \angle B &= \sin^{-1}\left ( \tfrac{b}{c} \right )=\:?\;^{\circ} \\ \end{align*}$

c) A's halveringslinje:

$\begin{align*} v_{nn}\text{ er vinkler med \textit{x}-aksen}: \\ \angle v_{A} &= -\left(\tfrac{\angle v_{AB}-\angle v_{AC}}{2}+\angle v_{AC}\right) =-\left(\tfrac{\angle v_{AB}+\angle v_{AC}}{2}\right) \\ \angle v_{A} &= \left(\tfrac{\tan^{-1}(-2)\, +\, \tan^{-1}(-0.5)}{2}\right)=-45^{\circ} \\ \tan\left(-45^{\circ}\right)=a_{v_A} &= -1 \\ v_A: y &= -x+b\Leftrightarrow b=y+x \\ b &= A_y+A_x \\ b &= 7+2=9 \\ y &= -x+9 \end{align*}$

d) a's median:

$\begin{align*} \text{Midtpunktet p\aa \,}BC&: \left(\tfrac{1}{2}\cdot (C_x-B_x)+B_x \, ,\,\tfrac{1}{2}\cdot (C_y-B_y)+B_y\right ) \\ D&: \left(8.5\, ,\,0\right ) \\ \tfrac{D_y-A_y}{D_x-A_x} &= \tfrac{0-7}{8.5-2}=a_{m_a}=-\tfrac{14}{13} \\ a_{m_a}: y &= -\tfrac{14}{13}x+b\Leftrightarrow b=y+\tfrac{14}{13}x \\ b &= A_y+\tfrac{14}{13}\cdot A_x \\ b &= 7+\tfrac{14}{13}\cdot 2=\tfrac{119}{13} \\ y &= -\tfrac{14}{13}x+\tfrac{119}{13} \;,\;A_x\leq x\leq D_x \\ y &= -\tfrac{14}{13}x+\tfrac{119}{13} \;,\;2\leq x\leq 8.5 \end{align*}$

e) a's højde:

$\begin{align*} \text{H\o jden p\aa \, \textit{a} er sammenfaldende med }AC:& \\ x+2y &= 16\;,\;A_x\leq x\leq C_x \\ x+2y &= 16\;,\;2\leq x\leq 10 \end{align*}$

Vedhæftet fil:__1.png

Brugbart svar (0)

Svar #14
26. maj 2019 af ringstedLC

Vedhæftet fil:__2.png

Brugbart svar (0)

Svar #15
27. maj 2019 af mathon

korrektion grundet grafforbytning:

$\small \begin{array}{llll} h_a\textup{ er et stykke}\\ \textup{af linjen }&\, \, \, \, \, \, \, \, \, \, \, \, \, x+2y=16\\\\ \textup{hvorfor h\o jden }\\ \textup{har samme ligning:}&h_a\textup{:}\quad x+2y=16\qquad 2\leq x\leq 10 \end{array}$

Skriv et svar til: Analytisk plangeometri - find punkterne for A, B & C

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.