Fysik

SERIE OG PARALLELKOBLING

29. juli 2019 af Trojanskhest - Niveau: B-niveau

Hej klogehoveder,

Jeg har følgende opgave

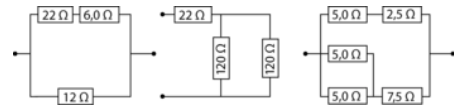
Bestem erstatningsresistansen i hver af de viste resistorkoblinger. (billedet er vedhæftet)

Mit problem er ikke formlerne, men mere at afgøre om der er tale om en serie eller parallel kobling.

Vedhæftet fil: Skærmbillede 2019-07-29 kl. 13.32.01.png

Brugbart svar (0)

Svar #1
29. juli 2019 af peter lind

Brugbart svar (0)

Svar #2
29. juli 2019 af mathon

$\small \begin{array}{lllll} \textup{bem\ae rk}&\textup{erstatningsmodstanden }&\textup{for to identiske}& \text{paralleltforbundne modstande }R&\textup{er }R_p=\frac{R}{2} \end{array}$

Brugbart svar (1)

Svar #3
29. juli 2019 af peter lind

Du er nød til at foretage sammensætningerne trinvis. Det er ikke bare enten parallel eller seriel kobling

a) De to øverste sættes samme serielt

Resultatet sættes parallet sammen med de 12Ω parallelt

b) De to til højre sættes sammer parallet

Resultatet sættes sammen serielt sammen med de 22 Ω

c)De to øverste sættes sammen seriel til erstatnngsmodstanden R1

De 2 nederst ti venstre på hver 5Ω sættes sammen parallelt til modstanden R2

R2 sættes sammen serielt med de 7,5Ω til modstanden R3

R1 og R3 sættes sammen parallet til facit R4

Brugbart svar (0)

Svar #4
29. juli 2019 af mathon

$\small \begin{array}{lllr} 1)&28\; \Omega \parallel \; 12\; \Omega =\frac{\left ( 28\; \Omega \right )\cdot \left ( 12\; \Omega \right )}{(28+12)\; \Omega }&=&8.4\; \Omega \\\\ 2)&\left ( 22\; \Omega \right )+\left ( 60\; \Omega \right )&=&82.0\; \Omega \\\\ 3)&\left (\left ( 5\; \Omega \right )+\left ( 2.5\; \Omega \right ) \right ) \parallel\left (\left ( 2.5\; \Omega \right )+\left ( 7.5\; \Omega \right ) \right )\\\\ &\left ( 7.5\; \Omega \right )\parallel\left ( 10\; \Omega \right )=\frac{\left (7.5\; \Omega \right )\cdot \left ( 10\; \Omega \right )}{\left (7.5+10 \right )\; \Omega }=\frac{75\; \Omega ^2}{17.5\; \Omega }&=&4.3\; \Omega \end{array}$

Brugbart svar (0)

Svar #5
29. juli 2019 af mathon

$\small \small \begin{array}{llllll} \textup{detaljer:}\\ &\frac{1}{R_p}=\frac{1}{R_1}+\frac{1}{R_2}\\\\ &\frac{1}{R_p}=\frac{R_2+R_1}{R_1\cdot R_2}\\\\ &R_p=\frac{{R_1\cdot R_2}}{R_1+R_2}\\\\\\\\ \textup{hvis }R_1\textup=R_2=R\\ &R_p=\frac{R^2}{2R}=\frac{R}{2} \end{array}$

Svar #6
29. juli 2019 af Trojanskhest

#4
$\small \begin{array}{lllr} 1)&28\; \Omega \parallel \; 12\; \Omega =\frac{\left ( 28\; \Omega \right )\cdot \left ( 12\; \Omega \right )}{(28+12)\; \Omega }&=&8.4\; \Omega \\\\ 2)&\left ( 22\; \Omega \right )+\left ( 60\; \Omega \right )&=&82.0\; \Omega \\\\ 3)&\left (\left ( 5\; \Omega \right )+\left ( 2.5\; \Omega \right ) \right ) \parallel\left (\left ( 2.5\; \Omega \right )+\left ( 7.5\; \Omega \right ) \right )\\\\ &\left ( 7.5\; \Omega \right )\parallel\left ( 10\; \Omega \right )=\frac{\left (7.5\; \Omega \right )\cdot \left ( 10\; \Omega \right )}{\left (7.5+10 \right )\; \Omega }=\frac{75\; \Omega ^2}{17.5\; \Omega }&=&4.3\; \Omega \end{array}$

Bless u

Brugbart svar (0)

Svar #7
30. juli 2019 af mathon

tilbagekobling:

https://www.studieportalen.dk/forums/thread.aspx?id=1904556

Skriv et svar til: SERIE OG PARALLELKOBLING

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.