Matematik

På linjen m

18. januar 2020 af NW12 - Niveau: B-niveau

Nogen som kan hjælpe med denne opgave? Jeg har prøvet at regne på den mange gange, men jeg forstår den ikke... tak på forhånd

Vedhæftet fil: ju.png

Brugbart svar (0)

Svar #1
18. januar 2020 af AMelev

a) Bestem ligningen for m.
Indsæt P(5,8) og tjek, at ligningen passer.

b) Omskriv parameterfremstillingen til x = ....... og y = ........
Indsæt x = 21 i den første ligning og løs den mht. t.
Indsæt så y = 1 og den fundne t-værdi i den sidste ligning og løs den mht. k
Indsæt evt. for en ordens skyld P(21,1) i m's ligning og tjek, at dette punkt også ligger på m.

Brugbart svar (0)

Svar #2
18. januar 2020 af ringstedLC

a) Lav en parameterfremstilling for linjen. Den har retningsvektoren:

$\begin{align*} \overrightarrow{r} &= \binom{B_x-A_x}{B_y-A_y}=\binom{a}{b} \\m: \binom{x}{y} &= \binom{A_x}{A_y}+t\cdot \binom{a}{b} \\ P:\binom{5}{8} &= \binom{A_x}{A_y}+t\cdot \binom{a}{b} \\ 5=A_x+t_1\cdot a&\wedge 8=A_y+t_2\cdot b \\ t_1 &= t_2\;? \end{align*}$

b) Brug igen koordinatfunktioner til at beregne k:

$\begin{align*} P:\binom{21}{1} &= \binom{3}{k}+t\cdot \binom{6}{2} \\ 21 &= 3+6t \\ t &= \;? \\ 1 &= k+2t \end{align*}$

Det er iøvrigt ligegyldigt for k, om P er skæringen mellem l og m.

Svar #3
18. januar 2020 af NW12

Jeg forstår det stadigvæk ikke helt, hvad er det jeg skal gøre i A)? Har prøvet alt det jeg har skrevet om parameterfremstilling, men det giver ikke mening....?

Brugbart svar (0)

Svar #4
19. januar 2020 af ringstedLC

Parameterfremstillingen kæver en retningsvektor og et punkt. Du har A og B som bruges til at danne en r.-vektor:

$\begin{align*} \binom{x}{y} &= \binom{x_0}{y_0}+t\cdot \binom{r_a}{r_b} \\ A&:\binom{-3}{4}\;,\;B:\binom{1}{5} \\ \overrightarrow{r} &= \binom{B_x-A_x}{B_y-A_y} \\ \overrightarrow{r} &= \binom{1-(-3)}{5-4}=\binom{4}{1} \end{align*}$

Punktet (x₀,y₀) kunne være A:

$\begin{align*} m:\binom{x}{y} &= \binom{-3}{4}+t\cdot \binom{4}{1} \end{align*}$

a) Redegørelse:

$\begin{align*} \binom{x}{y} &= \binom{-3}{4}+t\cdot \binom{4}{1}=\binom{-3}{4}+\binom{4t}{t} \\ x(t) &= -3+4t \\ y(t) &= 4+t \\ P&:\binom{5}{8}\text{ inds\ae ttes}: \\ 5 &= -3+4t_1\Leftrightarrow t_1=2 \\ 8 &= 4+t_2\Leftrightarrow t_2=4 \\ t_1 &\neq t_2 \end{align*}$

P opfylder ikke fremstillingen og ligger derfor ikke på m. En "snydeopgave"...

Brugbart svar (0)

Svar #5
19. januar 2020 af AMelev

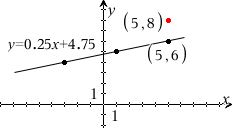
Ligning for m: y = 0.25x + 4.75, jf FS side 17 (80) & (81)
0.25·5 + 4.75 = 6 ≠ 8, så P(5,8) ligger ikke på m.

Vedhæftet fil:Udklip.JPG

Svar #6
19. januar 2020 af NW12

Okay. Tusind tak! Forstår det nu:)

Svar #7
19. januar 2020 af NW12

Tallet k, skal være 3 før linjerne l og m krydser hinanden, ikke?

Brugbart svar (0)

Svar #8
19. januar 2020 af ringstedLC

Se #2 b): Bestem t, indsæt værdien i ligningen nedenunder og bestem k.

Svar #9
19. januar 2020 af NW12

Jeg forstår det ikke, jeg kan jo ikke bare indsætte t, jeg kender jo stadig ikke mit k. Undskyld, men jeg forstår det ikke... kan godt være det er meget simplet, men ikke for mig..

Brugbart svar (0)

Svar #10
19. januar 2020 af AMelev

#7 Nej t = 3. k = -5 for P(21,1), men det punkt ligger ikke på m. Linjerne krydser ikke hinanden i P(21,1) uanset værdi af t og k.

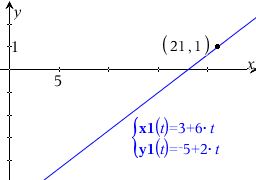
Der er noget helt galt med koordinatsættene for punkterne i forhold til opgavens ordlyd, men jeg kan ikke umiddelbartse, at det skyldes en simpel tastefejl.

Vedhæftet fil:Udklip.JPG

Svar #11
19. januar 2020 af NW12

Har lige tjekket og der er ikke tastefejl:).

Brugbart svar (0)

Svar #12
19. januar 2020 af ringstedLC

#9
Jeg forstår det ikke, jeg kan jo ikke bare indsætte t, jeg kender jo stadig ikke mit k. Undskyld, men jeg forstår det ikke... kan godt være det er meget simplet, men ikke for mig..

Du skal først bestemme t:

$\begin{align*} P:\binom{{\color{Red} P_x}}{{\color{Blue} P_y}}=\binom{{\color{Red} 21}}{{\color{Blue} 1}} &= \binom{{\color{Red} 3}}{{\color{Blue} k}}+{\color{Red} t}\cdot \binom{{\color{Red} 6}}{{\color{Blue} 2}} \\ {\color{Red} P_x}={\color{Red} 21} &= {\color{Red} 3}+{\color{Red} t}\cdot {\color{Red} 6} \\ 6t &= 21-3 \\ t &= 3 \\ {\color{Blue} P_y}={\color{Blue} 1} &= {\color{Blue} k}+{\color{Red} t}\cdot {\color{Blue} 2} \\ 1 &= k+3\cdot 2 \\ k &= -5 \end{align*}$

Værdien t skal være den samme for P_x og P_y for at P ligger på l.

#10: Enig, mærkelig opgave. Den er måske sakset sammen af en eller flere opgaver. Det virker også underligt, at der er to punkter, der hedder P i samme opgave.

Svar #13
19. januar 2020 af NW12

Tusind tak, nu giver det mening

Brugbart svar (0)

Svar #14
19. januar 2020 af AMelev

#11 Jeg mente ikke en tastefejl fra din side, men fra opgavestillerens.

Skriv et svar til: På linjen m

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.