Matematik

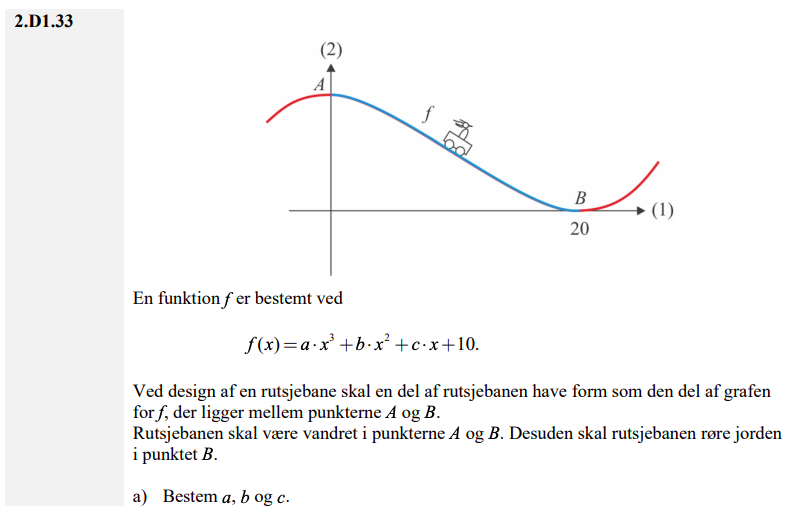
Bestemmelse af konstanterne i et tredjegradspolynomium. " Ved design af en rutsjebane ... "

25. januar 2020 af Kinkals - Niveau: A-niveau

Jeg bøvler lidt med denne opgave som skal løses UDEN brug af hjælpemidler.

Jeg har tidligere løst den selvsamme opgave MED hjælpemidler, hvor jeg løste 3 ligninger med 3 ubekendte som et ligningssystem vha. wordmat - piece of cake. Men uden hjælpemidler begriber jeg ikke hvordan opgaven kan løses.

Håber nogen kan komme mig til undsætning.

Tak på forhånd.

Vedhæftet fil: Skærmbillede 2020-01-25 kl. 01.42.48.png

Svar #1
25. januar 2020 af Kinkals

Brugbart svar (0)

Svar #2
25. januar 2020 af mathon

$\small \small \small \small \small \begin{array}{llll}&f(x)=a\cdot x^3+b\cdot x^2+c\cdot x+10\\\\&f{\, }'(x)=3a\cdot x^2+2b\cdot x+c\\\\\\&f(20)=0\\\\&0=a\cdot 20^3+b\cdot 20^2+c+10\\\\&0=8000a+400b+c+10\\\\\\&f{\,}' (0)=0=0+0+c\\\textup{hvoraf:}\\&c=0\\\\\\ &f{\, }'(20)=0 \\\\&0=3a\cdot 20^2+2b\cdot 0\\\\\\\textup{til bestemmelse }\\\textup{af }a \textup{ og }b\textup{ haves:}\\&\begin{Bmatrix} 0=8000a+400b+10\\ 0=1200a+40b \end{Bmatrix} \end{array}$

Brugbart svar (0)

Svar #3
25. januar 2020 af mathon

tastekorrektion:
$\small \small \small \small \small \small \begin{array}{llll}&f(x)=a\cdot x^3+b\cdot x^2+c\cdot x+10\\\\&f{\, }'(x)=3a\cdot x^2+2b\cdot x+c\\\\\\&f(20)=0\\\\&0=a\cdot 20^3+b\cdot 20^2+c+10\\\\&0=8000a+400b+c+10\\\\\\&f{\,}' (0)=0=0+0+c\\\textup{hvoraf:}\\&c=0\\\\\\ &f{\, }'(20)=0 \\\\&0=3a\cdot 20^2+2b\cdot \mathbf{{\color{Red} 20}}\\\\\\\textup{til bestemmelse }\\\textup{af }a \textup{ og }b\textup{ haves:}\\&\begin{Bmatrix} 0=8000a+400b+10\\ 0=1200a+40b \end{Bmatrix} \end{array}$

Brugbart svar (0)

Svar #4
25. januar 2020 af ringstedLC

To ligninger med to ubekendte (af 1. grad) ved substitution:

$\begin{align*} \text{I}:ax+by &= c\Rightarrow y=\;\left (...\right ) \\ \text{II}:fx+gy &= h \;,\;\text{ a\,-\,h er kendte konstanter} \\ fx+g\cdot \left (...\right ) &= h \\ x &= \;? \\ \text{Inds\ae t\,\textit{x} i I}:y &= \left (...\right ) \end{align*}$

Tre ligninger med tre ubekendte (af 1. grad) ved substitution:

$\begin{align*} \text{I}:ax+by+cz &= d\Rightarrow z=\;\left (...\right ) \\ \text{II}:fx+gy+hz &= j \\ \text{III}:kx+my+nz &= p \;,\;\text{ a\,-\,p er kendte konstanter} \\ \text{Inds\ae t\,\textit{z} i II og III}: \\ \left.\begin{matrix}fx+gy+h\cdot \left (...\right )=j \\ kx+my+n\cdot \left (...\right )=p \end{matrix}\right\}&\Rightarrow \text{to ligninger med to ubekendte} \\ \text{Inds\ae t (\textit{x},\,\textit{y}) i I}:\\ z &= \left ( ... \right ) \end{align*}$

Brugbart svar (0)

Svar #5
25. januar 2020 af mathon

$\small \begin{array}{lllllllll}&I\textup{:}&800a+40b=-1\\&II\textup{:}&30a+\, \, \, \, \, \,\, \, \, b=\, \, \, \, 0\\\\\\&&&D=\begin{vmatrix} 800&40 \\ 30&1 \end{vmatrix}=800-1200=-400\\\\&&&D_a=\begin{vmatrix} -1&40\\ 0&1 \end{vmatrix}=-1\\\\&&&D_b=\begin{vmatrix} 800&-1\\ 30&0 \end{vmatrix}=30\\\\&&&a=\frac{D_a}{D}=\frac{-1}{-400}=\frac{1}{400}\\\\ &&&b=\frac{D_b}{D}=\frac{30}{-400}=-\frac{3}{40}\end{array}$

Brugbart svar (0)

Svar #6
08. december 2021 af Maria200 (Slettet)

#3
tastekorrektion:
$\small \small \small \small \small \small \begin{array}{llll}&f(x)=a\cdot x^3+b\cdot x^2+c\cdot x+10\\\\&f{\, }'(x)=3a\cdot x^2+2b\cdot x+c\\\\\\&f(20)=0\\\\&0=a\cdot 20^3+b\cdot 20^2+c+10\\\\&0=8000a+400b+c+10\\\\\\&f{\,}' (0)=0=0+0+c\\\textup{hvoraf:}\\&c=0\\\\\\ &f{\, }'(20)=0 \\\\&0=3a\cdot 20^2+2b\cdot \mathbf{{\color{Red} 20}}\\\\\\\textup{til bestemmelse }\\\textup{af }a \textup{ og }b\textup{ haves:}\\&\begin{Bmatrix} 0=8000a+400b+10\\ 0=1200a+40b \end{Bmatrix} \end{array}$

Hvorfor regner du både den differentierede og den almindelige værdi af a, b og c ud?

Brugbart svar (0)

Svar #7
08. december 2021 af ringstedLC

Som det ses bruges f' til at opstille de to ligninger.

Brugbart svar (0)

Svar #8
09. december 2021 af mathon

a, b og c er konstanter, hvorfor der ikke findes "almindelige og differentierede værdier" af disse.

Skriv et svar til: Bestemmelse af konstanterne i et tredjegradspolynomium. " Ved design af en rutsjebane ... "

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.