Eksponentiel vækst

Jeg indsætter lige dit vedhæftede billede, det gør det nemmere at hjælpe:

hvor f(x) er motorcyklens værdi x år efter købet.

hvad mener du

#0
a) Jeg har lidt svært ved at se, at man skulle kunne bruge formler til at afgøre, hvilken model der bedst kan beskrive sammenhængen.
Lav et punktplot af tabellens data. Af plottet fremgår det tydeligt, at en lineær model ikke er god, da der er en systematisk afbøjning. Så kan man prøve en eksponentiel eller et 2.gradpolynomium.
Af lineær/eksponentiel, er den eksponentielle model klart bedst.Hvis I kun har arbejdet med lineære og eksponentielle modeller, kan du springe resten over og nøjes med at lave eksponentiel regression på datasættet, og så skulle du gerne få resultatet i #2.

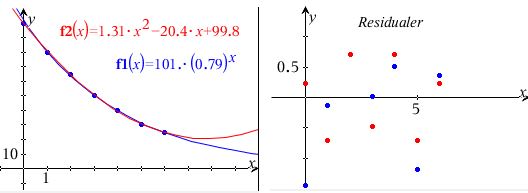
Hvis regressionsgraferne for de to typer tegnes i samme vindue som plottet, kan man se, at begge typer passer godt med punkterne, men hvilken der passer bedst er svært at afgøre umiddelbart.

Hvis man kigger på residualerne, ligger de, der hører til 2.gradspolynomiet, mest jævnt om x-aksen, hvilket kunne tale for, at det er den bedste model.
Det, der taler mod den er, at det ikke lyder troværdigt, at prisen allerede efter 7-8 år skulle begynde at vokse igen. På det tidspunkt er motorcyklen jo ikke i nærheden af veteranstatus.

b) Spørgsmålet er baseret på den eksponentielle model jf. #2.
Vækstraten r = a - 1.
Halveringstiden T_½ beregnes ud fra formlen for denne. 
Prisen efter 7 år: Beregn f(7)
Prisen 15000 kr. Løs ligningen f(x) = 15000

c) Spørgsmålet giver ikke rigtig mening i denne opgave, måske er det en "Kopi-pasta"-smutter.
Da f er en eksponentiel funktion med 0 < a < 1, er Dm(f) = R, Vm(f) = R₊ og f er aftagende uden ekstrema. 
Men da f er en modelfunktion er det ret uinteressant, da motorcyklen ikke kan have en negativ alder, og heller ikke kan forventes at holde evigt. Skrotalder og skrotpris kendes ikke, og man kan heller ikke forvente, at prismodellen holder mange år fremover.

tak for det