Matematik

Bestem x, så arealet at størst muligt.

26. marts 2020 af m1564 - Niveau: B-niveau

Hej!

Jeg har problemer med at finde ud af, hvordan jeg løser opgave b i vedhæftede billede.

Opgaven lyder:

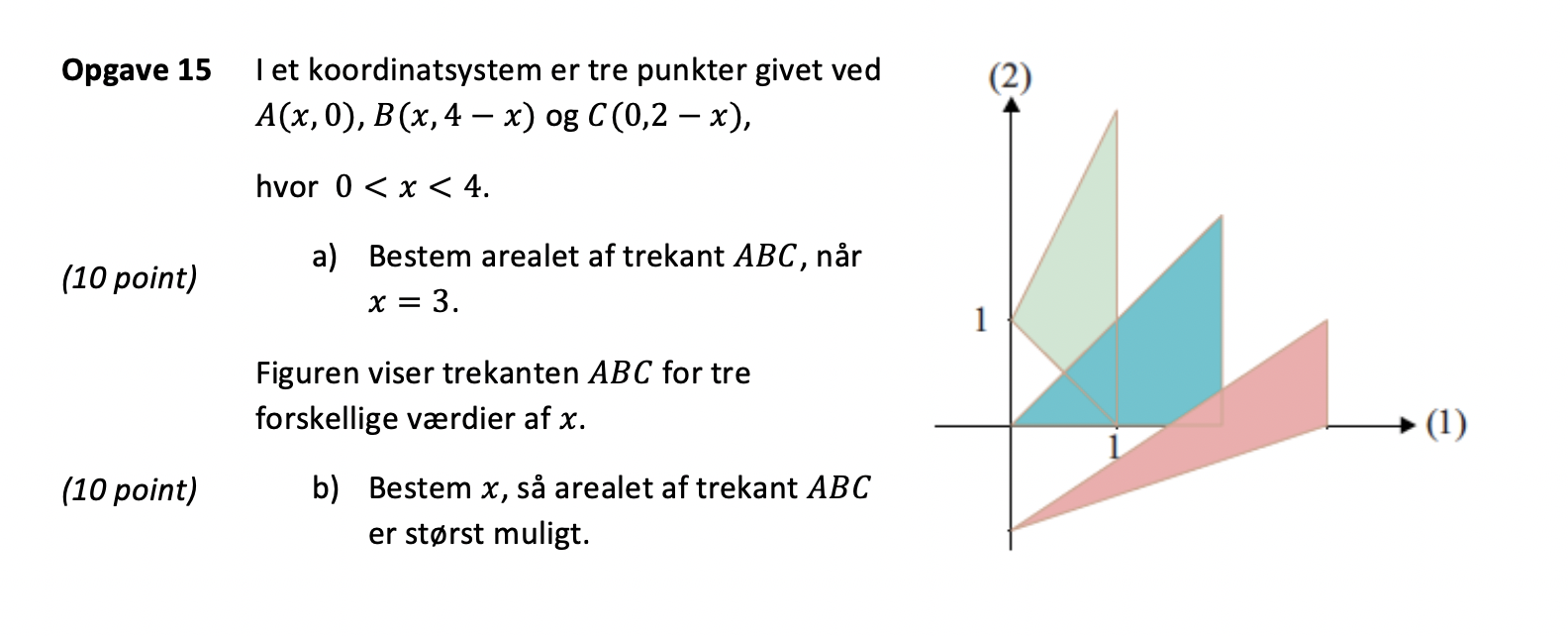
Bestem x, så arealet af trekant ABC er størst muligt.

Vedhæftet fil: Skærmbillede 2020-03-26 kl. 00.43.08.png

Brugbart svar (1)

Svar #1
26. marts 2020 af mathmadesimple

Det er en optimeringsopgave. Her skal du differentiere dit udtryk for arealet udtrykt ved x og bestemmet nulpunktet for dette udtrykt som om det var en afledt funktion

Brugbart svar (0)

Svar #2
26. marts 2020 af mathon

Brugbart svar (2)

Svar #3
26. marts 2020 af mathon

Højden er x og grundlinjen er 4-x
som for x = 3
giver trekantsarealet :

$\small \begin{array}{llllll}&T=\frac{1}{2}\cdot 3\cdot (4-3)=\frac{3}{2} \end{array}$

Den almene arealformel
bliver:
$\small \begin{array}{llllll}&T=\frac{1}{2}\cdot x\cdot (4-x)\\\\&T=-\frac{1}{2}x^2+2x \end{array}$
Maksimum
kræver bl.a.
$\small \begin{array}{llllll}&T{\, }'(x_o)=-x_o+2=0\\\\&x_o=2 \end{array}$
Fortegnsvariation
for $\small T{\,}'(x)$ : + 0 -
0________2________4
max

Trekantsarealet er størst for x = 2.

Brugbart svar (0)

Svar #4
21. september 2023 af CarlElias

Hvordan løser man den første opgave?

Brugbart svar (0)

Svar #5
24. september 2023 af mathon

#4
a) se
https://www.studieportalen.dk/forums/thread.aspx?id=2077080

Skriv et svar til: Bestem x, så arealet at størst muligt.

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.