Matematik

Areal af en trekant med skæv grundlinje og højde

27. marts 2020 af Mathmanden - Niveau: 9. klasse

Hej Studieportalen

Vi har fået nogle opgaver hvor vi skal ud for tre punkter i et krodinat system danne en trekant hvorefter regne arealet eller omkredsen.

For areal skal jeg vide hvad at grundlinjen og højden er. For omkredsen skal jeg minimum vide to af siderne.

Men jeg forstår ikke hvordan jeg skal regne en trekant hvor at grundlinjen ikke er lige.

Desuden forstår jeg heller ikke hvordan jeg kommer frem til omkredsen ud fra denne trekant.

Svar #1
27. marts 2020 af Mathmanden

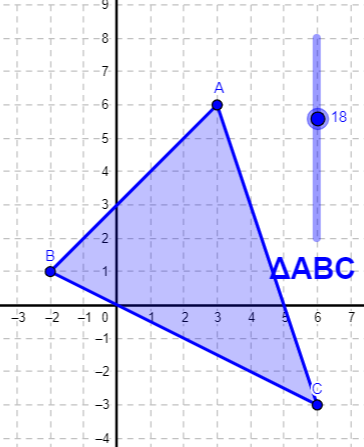
Ved ikke hvorfor at trekanten ikke kom med men den er her

Vedhæftet fil:Udklip.PNG

Brugbart svar (0)

Svar #2
27. marts 2020 af StoreNord

Trekantens sider kan du finde med Pythagoras.

For at finde arealet kan du tegne:
en retvinklet trekant under BC
en retvinklet trekant over BC
en retvinklet trekant over BC
Den samlede figur er så et rektangel, som du kan se arealet af.
Så trækker du de tre retvinklede trekanters areal fra rektanglets areal.

Brugbart svar (0)

Svar #3
27. marts 2020 af PeterValberg

Pythagoras' læresætning gælder for retvinklede trekanter, hvilket denne ikke er

Brug afstandformlen til at bestemme sidernes længde ud fra de givne koordinater.
Når du har bestemt sidernes længde, er omkredsen let at beregne.
Arealet bestemmer du med Heron's formel (googl' det)

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #4
28. marts 2020 af mathon

Brugbart svar (0)

Svar #5
28. marts 2020 af mathon

eller

Nummereres vinkelspidserne i positiv omløbsretning - uanset begyndelsesvinkelspids -
   beregnes trekantens areal:
   $\small T=\tfrac{1}{2}\cdot \left [ x_1\cdot (y_2-y_3)+x_2\cdot (y_3-y_1)+x_3\cdot (y_1-y_2) \right ]$
   Begyndes f.eks. med A
   har man:

$\small \begin{array}{lllllllllll}&x_1=3\qquad x_2=-2\qquad x_3=6\\\\&(y_2-y_3)=(1-(-3))=4&& y_3-y_1=-3-6=-9&& y_1-y_2=6-1=5\\\\&T=\frac{1}{2}\cdot \left [ 3\cdot 4+(-2)\cdot (-9) +6\cdot 5\right ]\\\\&T=\frac{1}{2}\cdot \left [ 12+18+30 \right ]=6+9+15\\\\&T=30 \end{array}$

Brugbart svar (0)

Svar #6
28. marts 2020 af mathon

Alternativt:
$\small \begin{array}{llll}&a=\sqrt{(6-(-2))^2+(-3-1)^2}=\sqrt{64+16}=\sqrt{80}\\\\&b=\sqrt{(6-3)^2+(-3-6)^2}=\sqrt{9+81}=\sqrt{90}\\\\&c=\sqrt{(3-(-2))^2+(6-1)^2}=\sqrt{5^2+5^2}=\sqrt{25+25}=\sqrt{50}\\\\\\&T=\frac{1}{4}\cdot \sqrt{a^2-(b-c)^2}\cdot \sqrt{(b+c)^2-a^2}\\\\&T=\frac{1}{4}\cdot \sqrt{80-\left (\sqrt{90}-\sqrt{50} \right )^2}\cdot \sqrt{\left (\sqrt{90}+\sqrt{50} \right )^2-80}\\\\&T=\frac{1}{4}\cdot8.61186\cdot 13.9343=30 \end{array}$

Brugbart svar (0)

Svar #7
28. marts 2020 af StoreNord

#2
Med "Trekantens sider kan du finde med Pythagoras."
mente jeg faktisk det samme, som du mener med "Afstandsformelen".

Herons Formel er god. Men jeg har indtryk af at mange elever ikke kender den.
Og slet ikke den i #6.

Brugbart svar (0)

Svar #8
28. marts 2020 af mathon

eller med
$\small \small \begin{array}{llll}&a=\sqrt{80}\\\\&b=\sqrt{90}\\\\&c=\sqrt{50}\\\\\\&T=\frac{1}{2}\cdot a\cdot b\cdot \sin(C)\\\\&T=\frac{1}{2}\cdot a\cdot b\cdot \sqrt{1-\cos^2(C)}\\\\&T=\frac{1}{2}\cdot \sqrt{80}\cdot \sqrt{90}\cdot \sqrt{1-\left (\frac{80+90-50}{2\cdot \sqrt{80}\cdot \sqrt{90}} \right) ^2}=30\end{array}$

Brugbart svar (0)

Svar #9
28. marts 2020 af mathon

Heron:
$\small \begin{array}{llll} &\textup{Define } s=\frac{\sqrt{80}+\sqrt{90}+\sqrt{50}}{2}\\\\&T=\sqrt{s\cdot \left (s-\sqrt{80} \right )\cdot \left (s-\sqrt{90} \right )\cdot \left (s-\sqrt{50} \right )}=30 \end{array}$

Brugbart svar (0)

Svar #10
29. marts 2020 af mathon

eller:
$\small \small \begin{array}{llllll}\textup{Det halve areal}\\\textup{udsp\ae ndt af }\\\textup{vektorerne }\overrightarrow{BA}\textup{ og }\overrightarrow{BC}\textup{:}&\overrightarrow{BA}=\begin{pmatrix} 3-(-2)\\6-1 \end{pmatrix}=\begin{pmatrix} 5\\5 \end{pmatrix}\qquad \overrightarrow{BC}=\begin{pmatrix} 6-(-2)\\-3-1 \end{pmatrix}=\begin{pmatrix} 8\\-4 \end{pmatrix}\\\\&T=\frac{1}{2}\cdot \begin{Vmatrix} 5 &8 \\ 5& -4 \end{Vmatrix}=\frac{1}{2}\cdot \left | 5\cdot (-4)-5\cdot 8 \right |=\frac{1}{2}\cdot \left | -20-40\right | =\frac{1}{2}\cdot 60=30 \\\\\\\textup{kontroltastet:}&\frac{1}{2}\cdot abs\left ( det\left ( \begin{bmatrix} 5 &8 \\ 5 &-4 \end{bmatrix} \right ) \right ) \end{array}$

Brugbart svar (0)

Svar #11
30. marts 2020 af PeterValberg

#7 Okay, det giver mening :-)

Heron's formel er ellers med i folkeskolens formelsamling < LINK > (side 24)

- - -

mvh.

Peter Valberg
(YouTube)

Skriv et svar til: Areal af en trekant med skæv grundlinje og højde

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.