Matematik

Forklare den grafiske betydning af løsningerne

29. marts 2020 af K22 - Niveau: A-niveau

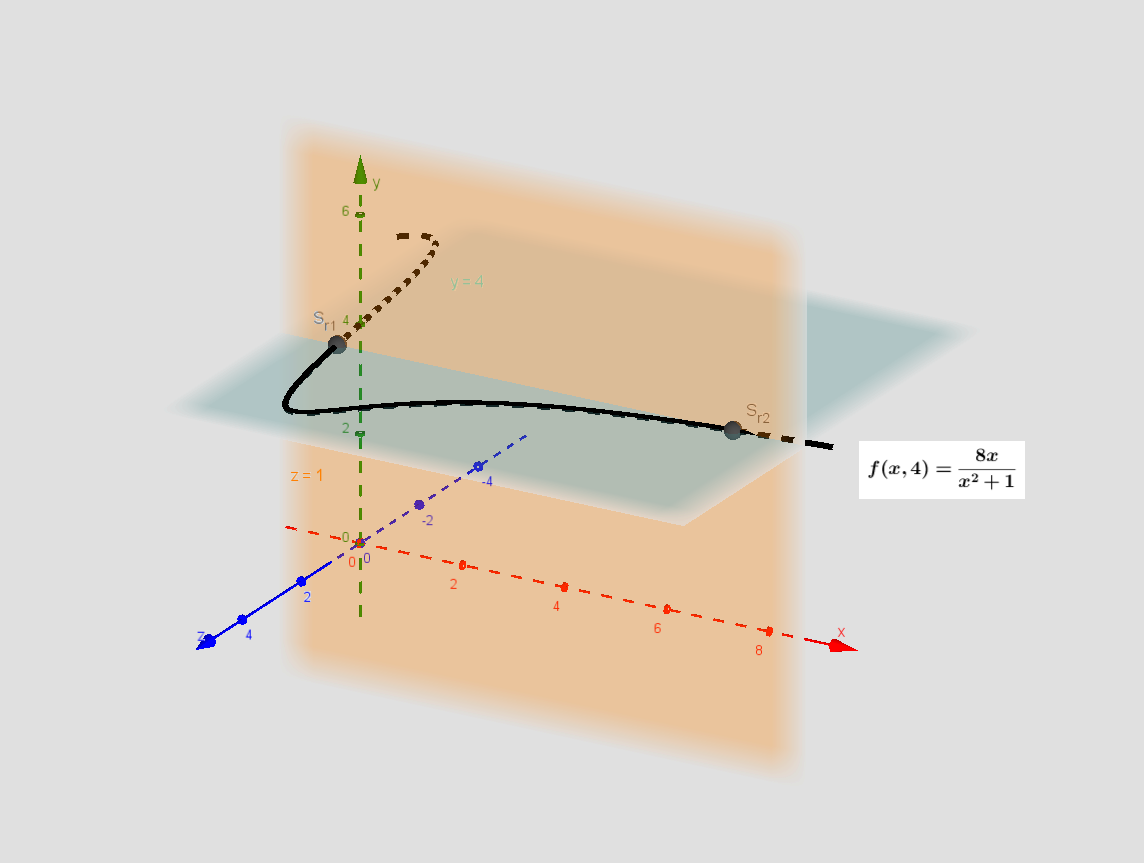
Til c). Kunne en besvarelse se sådan her ud?

Løsningerne er x = -1 V x = 3. f(x, 4) = 1 har to lodrette linjer x = -1 og x = 3.

Vedhæftet fil: Skærmbillede 2020-03-29 kl. 18.49.31.png

Brugbart svar (0)

Svar #1
29. marts 2020 af ringstedLC

Se lige svaret i: https://www.studieportalen.dk/forums/thread.aspx?id=1948138#1948169 igen.

I 2D er x = -1 en ret linje parallel med y-aksen. I 3D er x = -1 en plan, der er parallel med yz-planen.

$\begin{align*} f(x,4)=1 &= \frac{2x\cdot 4}{x^2+1}\neq \frac{2x\,{\color{Red} +}\, 4}{x^2+1} \\x &= \left\{\begin{matrix} 4-\sqrt{15}\approx 0.13\\ 4+\sqrt{15}\approx 7.87 \end{matrix}\right. \end{align*}$

Man kunne sige, at løsningerne giver skæringspunkterne:

$\begin{align*} S_{r_1}=\left (4-\sqrt{15},4,1 \right ) \\ S_{r_2}=\left (4+\sqrt{15},4,1 \right ) \end{align*}$

mellem snitfunktionen til f , y = 4 og planen z = 1.

Vedhæftet fil:A_M_094 - Multivar. fkt._1948539_K22.png

Skriv et svar til: Forklare den grafiske betydning af løsningerne

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.