Matematik
Brug for hjælp til forståelse og udregnelse af forskrifts bestemmelse med graf
Man har registreret verdensrekorder for skihop siden 1808, hvor en nordmand hoppede 9,5 meter. Siden er rekorden blevet slået mange gange.
Filen Hoplængde viser verdensrekorder i perioden 1879 - 2017.
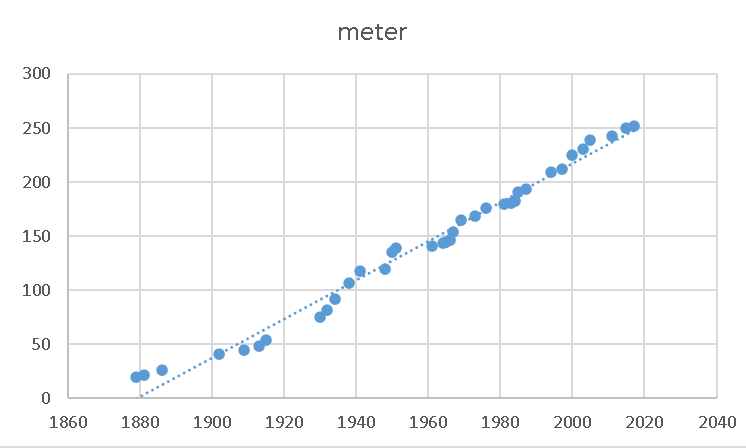
f) Indtegn data i et koordinatsystem.
Hoplængden L måles i meter, og tiden t måles i år efter 1879.
En model for sammenhængen mellem L og t, kan beskrives ved en funktion l.
g) Bestem en forskrift for l.
Modellen bestemt i g) indeholder et antal parametre.
h) Forklar betydningen af disse parametre.
i) Hvornår kan man forvente, at rekorden vil runde 270 m ifølge modellen?
j) Er det realistisk at benytte modellen for det længste hop i 1808? Svaret skal begrundes både grafisk og ved beregning.
Jeg har allerede lavet F men jeg har virkelig brug for hjælp til G
Svar #2
27. april 2020 af peter lind
Brug regression på de data, hvis du ikke allerede har gjort det
Svar #3
27. april 2020 af ISwallowYoPapa
jeg har brugt en linær regressions linje
Svar #4
27. april 2020 af AMelev
Den skulle du da have lagt op i det første billede. Du har jo fået modellen via regressionen.
l(t) = 1.7959·t - 3374.5
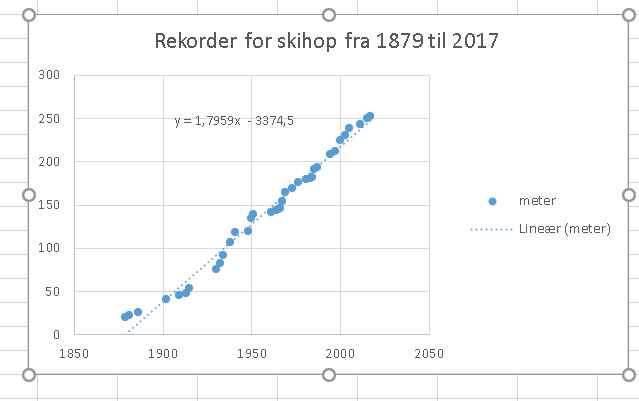
Er alle dine problemer løst nu? Ellers må du vende tilbage.
Måske kunne en eksponentiel sammenhæng også være i spil. Det kunne du jo overveje.
Svar #6
27. april 2020 af ISwallowYoPapa
mange tak men kan jeg godt lige fået foklaret betydningen med parametrene ved det ikke helt
undskyld for at jeg lyder virkelig dum har bare siddet oppe hele natten med lektier
Svar #8
27. april 2020 af AMelev
Ups! Jeg havde ikke nærlæst. Undskyld!
Hoplængden L måles i meter, og tiden t måles i år efter 1879.
Der er nu to muligheder
1) Du laver en ny t-liste "Årstal - 1879" og en ny regression over (x,L)
2) Du har fra regressionen f(x) = y = 1.7959·x - 3374.5, hvor x = Årstal, og t = x - 1879 ⇔ t = x + 1879
og så tilpasser du funktionen ved at sætte x ind i y: l(t) = 1.7959·(t + 1879) - 3374.5 = ....
En lineær model er nok ikke så god, da det giver en negativ længde på et hop, men det er lidt svært at vurdere, når vi ikke har data.
Kan du ikke lige uploade dem.
Svar #9
28. april 2020 af christensen19
Har samme opgave. her er dataen
Svar #10
28. april 2020 af AMelev
Den lineære model er den bedste, så hold fast i den.
Med korrektionen for t = Antal år efter 1879 og med l(t) = længde/m fås
l(t) = 1.7959·x + 0.
Parameteren b = 0 angiver, at verdenrekorden for skihop iflg. modellen var 0 meter i 1879.
Hældningskoefficienten a = 1.7959 angiver, at rekorden siden da er steget med 1.8 meter om året iflg. modellen.
Svar #14
28. april 2020 af peter lind
Nej. Hvis du sætter x = 1879 eller 0 i den korrigerede model får du 0 m
Svar #15
28. april 2020 af AMelev
#13 Læs de svar, der gives, omhyggeligt.
#10
Parameteren b = 0 angiver, at verdenrekorden for skihop iflg. modellen var 0 meter i 1879.
#12
i) Løs ligningen l(t) = 270 mht. t.
j) Kan du ikke selv svare på det? 1808 er 71 år før 1879, så t = -71. Hvilke resultater giver det for verdensrekorden?
Svar #17
28. april 2020 af AMelev
Du har en forskrift for l(t).
i) Ved du ikke, hvordan du løser en ligning?
j) Ved du ikke, hvordan du bestemmer en funktionsværdi ved beregning og ved grafisk aflæsning?
Svar #18
28. april 2020 af christensen19