Geometri

Lave din opgave? .... NEJ

Hjælpe dig med din opgave? .... Ja
...du kan nemlig få noget hjælp toil selvhjælp,
du kan se videoerne nr. 30 - 34 på denne videoliste < LINK >

Cirklens ligning betegnes ofte som "Pythagoras i anvendelse".

De videoer er jo elendige. 

Mathon du plejer altid at være en chef, og lave opgaver ://

#3 Det er så din mening, mon ikke det hænger sammen med,
     at du hellere vil have os til at levere en færdig besvarelse
     fremfor selv at skulle gøre noget aktivt....

Giv nu de videoer en chance, - du kunne risikere at lære noget nyttigt :-)

Jamen forhelvede Peter, har lige set 3 af videorne og det fiser lige ud af det andet øre. 

Tegn et koordinatsystem.

Indtegn heri med centrum i (a,b) - vælges vilkårligt - en cirkel med vilkårlig radius r.

Vælg og afmærk et vilkårligt punkt på cirkelperiferien.

Tegn radius fra cirkelcentrum til det valgte punkt.

Afmærk det valgte punkts projektion på en linje gennem cirkelcentrum parallel med x-aksen.

Betragt trekanten med vinkelspidser i cirkelcentrum, det afmærkede punkt på cirkelperiferien og projektionspunktet.

Betragt trekanten med vinkelspidser i cirkelcentrum (a,b), det afmærkede punkt på cirkelperiferien (x,y) og projektionspunktet (x,b).

#1.

En tangent for en kurve (grafen for en funktion eller evt. en cirkel) kan defineres ud fra en sekant. Man vælger et fastholdt punkt på kurven og trækker en ret linje gennem dette og et variabelt punkt på kurven. Denne rette linje kaldes en sekant. Man lader det variable punkt nærme sig det fastholdte punkt og undersøger om sekanten nærmer sig en bestemt ret linje. Dette gentages for et variabelt punkt, der ligger på den anden siden af det faste punkt for at sikre sig at der ikke er et knæk på kurven. Hvis de to sekanter går mod samme rette linje, så kaldes denne rette linje for tangenten til kurven i det faste punkt (tangentpunktet). 

Cirklens ligning er (x-a)² + (y-b)² = r², hvor a og b er koordinaterne til cirklens centrum og r er cirklens radius.

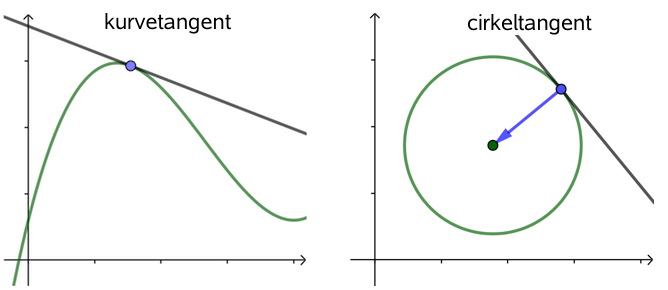
Tangenten til en cirkel står vinkelret på en radius i cirklen. Denne radius er normalvektor til tangenten. Ud fra dette kan man finde tangentens ligning. Cirklens centrum kaldes C, tangentpunktet kaldes P og et vilkårligt punkt på tangenten kaldes Q = (x,y). Der gælder for vektoren PC og vektoren PQ, at PC·PQ = 0. Ved at indsætte koordinaterne for punkterne, så får man tangentens ligning udtrykt i x og y.

Eksempler på tangenter: 

En tangent er en ret linje gennen røringspunktet (x_o,y_o) og med f'(x_o) som hældningstal, hvorfor 
punkt-hældningsformlen kan anvendes: